非参数检验丨Friedman’s test （多配对样本）

什么是Friedman检验？

Friedman检验是一种非参数检验，也叫M检验，是重复测量方差分析的非参数检验版本，是Kruskal-Wallis检验的配对样本版本，可以认为是用于两组配对的符号检验的扩展，用于比较三个或更多配对的研究组。由美国经济学家Milton Friedman在1937年提出。

Friedman检验的适用条件

1. 适用于非正态分布的数据，正态分布请用重复测量方差分析

2. 当有**三个或更多**配对样本（或处理）需要比较时（例如，同一组受试者在不同条件下的测量值，在不同时间的测量值）。

   1. 三个或更多独立样本请用Kruskal-Wallis检验
   2. 两个配对样本请用sign test（符号检验）或Wilcoxon Signed Rank Test

3. 数据是序数类型或连续类型

何时使用Friedman检验?

Friedman检验通常用于两种情况：

1. 测量受试者在三个或更多时间点的平均分数。

例如，您可能想要在开始训练计划前一个月、开始计划后一个月以及使用计划后两个月测量受试者的剩余心率。可以进行Friedman检验，看看患者在这三个时间点的平均剩余心率是否存在显着差异。

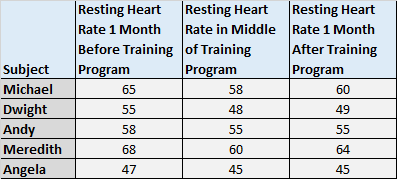
2. 测量受试者在三种不同条件下的平均分数。

例如，您可能会要求受试者观看三部不同的电影，并根据他们对电影的喜爱程度对每部电影进行评分。由于每个主题都出现在每个样本中，因此可以进行Friedman检验来查看三部电影的平均评分是否存在显着差异。

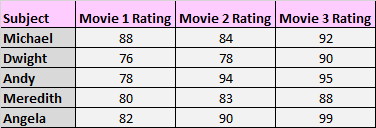
Friedman检验的基本步骤

Friedman检验首先从低到高排列每行（区块）不同处理中的值。每一行均分开排列。然后对每个处理（列）中的秩求和。如果总和相差很大，则P值会很小。

1️⃣ 数据排序：对每个受试对象的k个观测值单独进行排序,赋予秩次1到k。

是对每个对象的观测值单独进行排序，不能像Kruskal-Wallis法那样将所有样本放在一起排序

然后计算各处理的秩和:

$$R_j = \sum_{i=1}^n R_{ij}$$

其中$R_j$是第j个处理的秩和,$R_{ij}$是第i个受试对象在第j个处理下的秩次。

2️⃣ 计算Friedman统计量$Q$:

公式

$$Q = \frac{12}{nk(k+1)} \sum_{j=1}^k R_j^2 - 3n(k+1)$$

其中:

• $n$是受试对象数量
• $k$是处理方法数量
• $R_j$是第j个处理的秩和

如果样本中存在结值（相同秩次），需要调整公式中的 Q 统计量，校正公式为:

$$Q_{corrected} = \frac{Q}{1 - \frac{\sum (t_i^3 - t_i)}{n(k^3 - k)}}$$

其中$t_i$是第 $i$ 个结值的个数。

3️⃣ 显著性检验：在显著性水平α下，如果计算得到的$Q$统计量大于临界值，则拒绝零假设，认为至少有两种处理方法的效果存在显著差异。

当 ${\textstyle n}$ 或 ${\textstyle k}$ 较大（即 ${\textstyle n>15}$ 或 ${\textstyle k>4}$ ）时， ${\textstyle Q}$ 的概率分布可以近似为卡方分布，$Q$统计量近似服从自由度为k-1的卡方分布，p值= ${\displaystyle \mathbf {P} (\chi _{k-1}^{2}\geq Q)}$ 。

如果 ${\textstyle n}$ 或 ${\textstyle k}$ 较小，卡方近似效果变差，应从专门为 Friedman 检验准备的 ${\textstyle Q}$ 表中获取$p$值。

4️⃣ 如果进行Friedman检验后发现呈现出显著性，因而可考虑继续对比两两处理之间的差异性。

常用的多重比较方法

• Dunn检验（GraphPad Prism默认使用）
• Nemenyi检验
• Conover 检验

‍

Friedman检验和Kruskal-Wallis检验区别？

• Friedman检验用于比较三个或更多相关样本的中位数差异。它是重复测量方差分析的非参数替代方法。
• 而Kruskal-Wallis检验是用于比较三个或更多独立样本的中位数差异。它是单因素方差分析的非参数替代方法。

Friedman检验的具体例子

小样本例子

根据三项指标评价四个小流域的水环境质量。希望知道这四个流域的水环境质量有没有明显差别。

以得分表示的评价结果为：

这是样本量为3的4个相关样本。有：

处理方法 k=4

受试对象 n=3

由于样本量很小且测量水平较低(仅仅是离散评分)，应当采用检验相关样本大小的Friedman秩方差分析。检验的原假设为：

H0：四个流域的水环境质量无明显差别，

H1：四个流域的水环境质量有明显差别。

分别对三项指标得分(4个)独立排序，求秩。然后计算各样本秩和$R_j$

计算检验统计量如下：

$$Q=\frac{12}{(3)(4)(5)}\left(11^2+5^2+4^2+10^2\right)-(3)(3)(5)=7.4$$

由于样本量较小，不宜直接使用卡方检验。

精确计算得到pvalue = 0.0330

因此可以在0.05显著性水平条件下拒绝检验的原假设。由此可见，四个流域的水环境质量有明显差别。

大样本例子

例2 作为大样本的例子，仍采用上例的方式检验三座城市大气质量有没有显著差异。测试了与大气质量有关的18项指标，下表列举了评分结果：

对以上结果排序得到的秩数据及秩和为：

为检验以下原假设：

H0：三城市大气质量没有明显差异，

H1：三城市大气质量有明显差异，

计算：

$$Q = \frac{12}{nk(k+1)} \sum_{j=1}^k R_j^2 - 3n(k+1)$$

因为n=18，k=3，所以

$$Q=\frac{12}{(18)(3)(4)}\left(38.5^2+43.5^2+26^2\right)-(3)(18)(4)=9.0278$$

由于存在结值，需要进行纠正

$$Q_{corrected} = \frac{Q}{1 - \frac{\sum (t_i^3 - t_i)}{n(k^3 - k)}}$$

数据中可以看到，只有指标15出现了结值（城市1和城市2的秩都是2.5）。

因为有2个相等的值，所以

$\sum (t_i^3 - t_i)= 1^3-1+2^3 - 2 = 6$

现在我们可以计算纠正后的Q值：

$$Q_{corrected} = \frac{9.0278}{1 - \frac{6}{18(3^3 - 3)}} = \frac{9.0278}{1 - \frac{6}{432}} = \frac{9.0278}{0.9861} = 9.155$$

因样本量较大，可直接根据自由度为2的$\chi^2$分布计算pvalue，pvalue = 0.0103<0.05

故拒绝检验的原假设，接受备选假设，认为三城市大气质量有明显差异

Friedman检验实现

Matlab

官方有提供friedman函数，但是不推荐，因为输入需要two way ANOVA的长表格格式，并且计算p值只能靠卡方近似计算，不能精确计算。

推荐用第三方的MyFriedman函数

GraphPad Prism

教程：Tutorial for : GraphPad Friedman test 教學 (youtube.com)

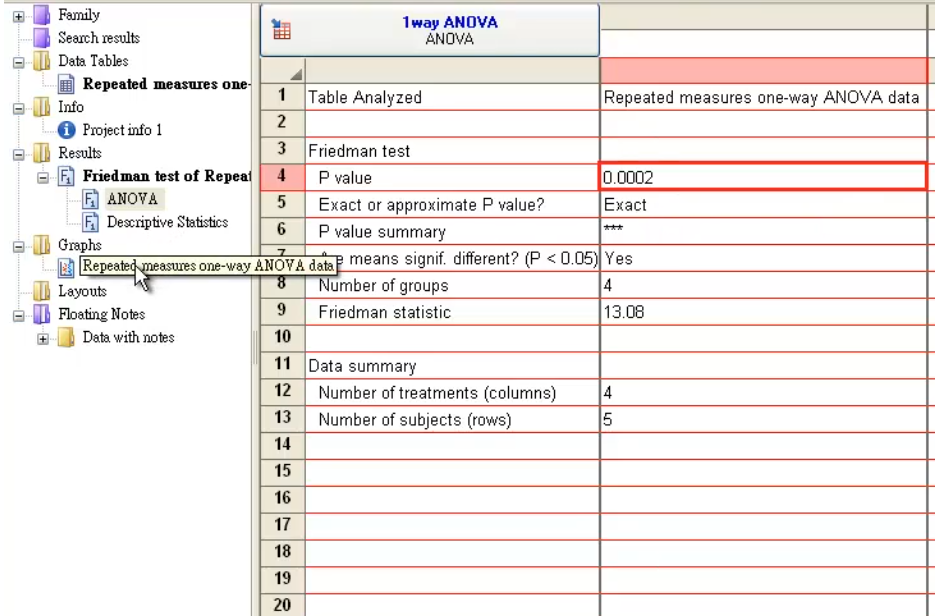
Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

import numpy as np
from scipy.stats import friedmanchisquare

# 数据
data = np.array([
    [2, 7, 5],
    [5, 6, 1],
    [4, 8, 7],
    [1, 4, 8],
    [6, 2, 5],
    [7, 8, 4],
    [6, 4, 2],
    [1, 9, 8],
    [9, 2, 4],
    [7, 3, 5],
    [5, 6, 2],
    [3, 4, 1],
    [6, 9, 5],
    [7, 8, 4],
    [6, 6, 3],
    [9, 7, 6],
    [6, 3, 2],
    [2, 5, 1]
])

# 进行Friedman检验
stat, p = friedmanchisquare(data[:, 0], data[:, 1], data[:, 2])

# 输出结果
print(f"Friedman检验统计量: {stat}")
print(f"p值: {p}")

if p < 0.05:
    print("结果显著，城市之间的评分有显著差异。")
else:
    print("结果不显著，城市之间的评分没有显著差异。")

参考资料

• 多独立样本Kruskal-Wallis检验-SPSSPRO帮助中心
• Friedman test - Wikipedia