非参数检验丨Kruskal-Wallis检验（多独立样本单因素）

什么是Kruskal-Wallis 检验？

Kruskal-Wallis 检验，也称作H检验，是一种非参数的假设检验方法，用于检验三组或以上样本中是否至少有一组的中位数存在显著不同。

Kruskal-Wallis 检验是ANOVA单因素方差分析的非参数检验版本，对数据的分布特征没有前置要求，且可以应用于顺序性变量的分析。多组独立样本如果检验正态性不符合时，选用Kruskal-Wallis 检验，如果是多组配对样本的非参数检验则用Friedman 检验。

Kruskal-Wallis 检验是 Mann-Whitney U test 的扩展。对于非参数检验，分析两组独立样本，应使用Mann-Whitney U检验，对于分析三组及以上独立样本，应该用Kruskal-Wallis 检验。

如果进行Kruskal-Wallis检验后发现呈现出显著性，可进行多重比较，对比两两组别之间的差异性。多重比较方法有Dunn检验、Nemenyi检验、Conover 检验等。

适用条件

数据类型：适用于三组或更多独立样本，且数据是连续或有序的。不适用于重复测量或配对设计的数据， 对于这类数据，应考虑使用Friedman检验。
假设：假设每个样本来自相同的分布，但不要求数据是正态分布的。

Kruskal-Wallis 检验的基本原理

多独立样本 Kruskal-Wallis 检验的基本步骤是：

首先，将多组样本合并，按从小到大排列，计算每个样本的秩和。

然后，考察各组秩的均值是否存在显著差异。如果各组秩的均值不存在显著差异，则认为多组数据充分混合，数值相差不大，可以认为多个总体的分布无显著差异；反之，如果各组秩的均值存在显著差异，则是多组数据无法混合，有些组的数值普遍偏大，有些组的数值普遍偏小，可认为多个总体的分布存在显著差异，至少有一个样本不同于其他样本。

为研究各组的秩差异，可借鉴方差分析的方法。

方差分析认为，各样本组秩的总方差一方面源于各样本组之间的差异（组间差），另一方面源于各样本组内的抽样误差（组内差）。如果各样本组秩的总方差的大部分可由组间差解释，则表明各样本组的总体分布存在显著差异；反之，如果各样本组秩的总方差的大部分不能由组间差解释，则表明各样本组的总体分布没有显著差异。

由上可以得出多独立样本非参数检验的目的（由独立样本数据推断多组样本的分布是否存在显著差异），基本假设（H0：多组分布无显著差异），数据要求（样本数据和分组标志）。

基于以上思路可以构造 H 统计量，即

H=\frac{\text { 秩的组间差平方和 }}{\text { 秩的总方差 }}

注意：ANOVA方差分析 F=组间差/组内差

需要检验的原假设为各组之间不存在差异，或者说各组的样本来自的总体具有相同的中心或均值或中位数。在原假设为真时，各组样本的秩平均应该与全体样本的秩平均 $\frac{1+2+\cdots+N}{N}=\frac{N+1}{2}$ 比较接近。

所以秩的组间差平方和为:

\text { 秩的组间差平方和 }=\sum_{i=1}^k n_i\left(\frac{R_i}{n_i}-\frac{N+1}{2}\right)^2

秩的组间差平方和除以全体样本秩方差，可以消除量纲的影响。样本方差的自由度为 n-1。所以

\begin{gathered} \text { 秩的总方差 }=\frac{1}{N-1} \sum_{i=1}^k \sum_{j=1}^N\left(R_{i j}-\frac{N+1}{2}\right)^2=\frac{1}{N-1} \sum_{i=1}^N\left(i-\frac{N+1}{2}\right)^2=\frac{1}{N-1}\left(\sum_{i=1}^N i^2-\frac{N(N+1)^2}{4}\right)= \\ \frac{1}{N-1}\left(\frac{N(N+1)(2 N+1)}{6}-\frac{N(N+1)^2}{4}\right)=\frac{N(N+1)}{12} \end{gathered}

因此，Kruskal-Wallis 秩和统计量 H 为

H=\frac{\text { 秩的组间差平方和}}{\text { 秩的总方差}}=\frac{12}{N(N+1)} \sum_{i=1}^k n_i\left(\frac{R_i}{n_i}-\frac{N+1}{2}\right)^2=\frac{12}{N(N+1)} \sum_{i=1}^k \frac{R_i{ }^2}{n_i}-3(N+1)

其中 $k$ 为样本组数， $N$ 是总样本量， $n_i$ 是第 $i$ 组的样本量； $R_i$ 是第 $i$ 组样本中的秩总和， $R_{ij}$ 是第 $i$ 组样本中的第 j 个观察值的秩值。

Kruskal-Wallis 检验的基本步骤

Kruskal-Wallis 检验的实现步骤如下：

提出零假设和备择假设
- 零假设：所有组的总体分布相同
- 备择假设：至少有一组的总体分布不同
将多组样本合并，按从小到大排列，计算每个样本的秩和 $R_i$
计算Kruskal-Wallis检验统计量 $H$ ，根据自由度和显著性水平查找Kruskal-Wallis检验临界值表，确定检验水平下的显著性水平，判断是否拒绝零假设
$H = \frac{12}{N(N+1)} \sum_{i=1}^{k} \frac{R_i^2}{n_i} - 3(N+1)$
其中， $N$ 是所有样本数量的总和， $n_i$ 是第 $i$ 组样本的数量， $R_i$ 是第 $i$ 组样本的秩和。

如果样本中存在结值（相同秩次），需要调整公式中的 K-W 统计量，校正系数 C 为:
$H_{corrected} = \frac{H}{1 - \frac{\sum (t_i^3 - t_i)}{N^3 - N}}$
其中 $t_i$ 是第 $i$ 个结值的个数。

如果每组样本中的观察数目至少有 5 个，那么样本统计量 H 非常接近自由度为 k-1 的卡方分布。因此，用卡方分布来决定 H 统计量的检验。

H统计量越大，p值越小
如果进行Kruskal-Wallis检验后发现呈现出显著性，因而可考虑继续对比两两组别之间的差异性。

多重比较怎么选择呢？

主流方法
- Dunn检验（最多人用）
- Nemenyi检验（也很多人用）
- Conover 检验（据说更强大，但是很少人用）
GraphPad Prism默认使用Dunn检验来做Kruskal-Wallis检验的多重比较

Kruskal-Wallis 检验和Mann-Whitney U检验区别

Mann-Whitney U检验用于比较两组独立样本，通过计算U统计量来进行检验。U统计量实际上是一种计数统计量。它代表了在两个样本中，一个样本的值大于另一个样本的值的次数。
Kruskal-Wallis 检验用于比较三组及更多组独立样本，计算H统计量来进行检验。H统计量借鉴了方差分析的思想，计算秩的组间差平方和除以秩总方差的平均。如果各样本组秩的总方差的大部分可由组间差解释，则表明各样本组的总体分布存在显著差异；反之，如果各样本组秩的总方差的大部分不能由组间差解释，则表明各样本组的总体分布没有显著差异。

效应大小Effect size

与只能告诉你是否存在统计显著差异或关系的 p 值不同，效应量旨在回答“这种差异或关系的强度如何？”这一问题。

Kruskal-Wallis 检验的效应量可以用Eta Squared (**** $\eta^2$ )指标量化， $\eta^2$ 指标可以通过以下公式计算：

Eta Squared (**** $\eta^2$ ) 可以通过以下公式计算：

\eta^2 = \frac{H - k + 1}{N - k}

其中 $H$ 是 Kruskal-Wallis 统计量， $k$ 是组数， $N$ 是总样本量。

例子

例子1 A、B两种菌对小鼠巨噬细胞吞噬功能的激活作用

Kruskal wallis检验案例分析_进行_n_i_数据 (sohu.com)

在一项动物实验中，研究者欲研究A、B两种菌对小鼠巨噬细胞吞噬功能的激活作用，将59只小鼠随机分为三组，其中一组为生理盐水对照组，用常规巨噬细胞吞噬细胞吞噬功能的检测方法。试比较不同实验条件下小鼠巨噬细胞的吞噬率有无差别？如果有差别具体进行分析下。

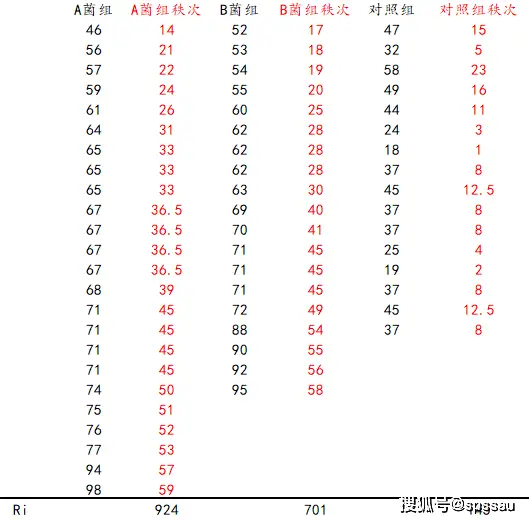
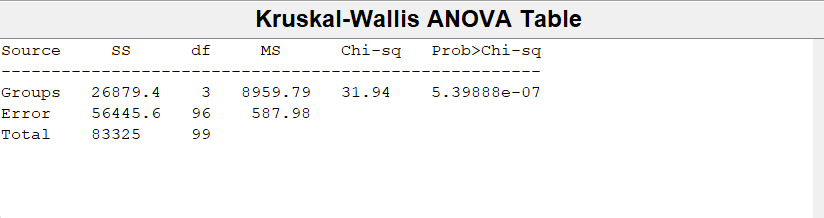
从上表可以得出，三组的吞噬率统计量H值为32.807，p值小于0.05.所以具有显著性差异。Kruskal wallis检验的统计量计算过程如下：

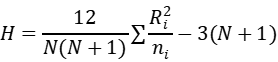
本例的数据具体计算过程如下：

其中样本共有59个，所以计算如下：

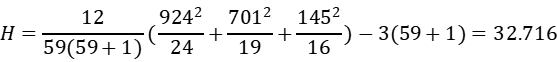
由于相同秩次较多，所以统计量需要进行校正。

H^{\prime}=\frac{H}{1-\sum_{i=1}^{m}T_{i}/(N^{3}-N)}=31.716/(1-0.002776)=32.807;

式中，m为结集的数量， $T_{i}= t_{i}^3- t_{i}$ 。

既然模型显著，进行进一步分析每两组之间是否存在差异？使用Nemenyi方法进行分析，分析结果如下：

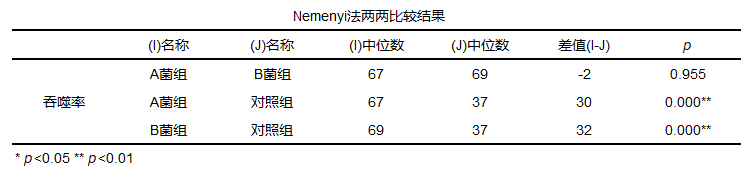
从结果可以看出，A菌组和B菌组p值为0.955>0.05,所以A菌组和B菌组之间并没有显著性差异，但是A菌组和对照组的p值远小于0.05，所以A菌组和对照组具有显著性差异，B菌组和对照组也同理。

‍

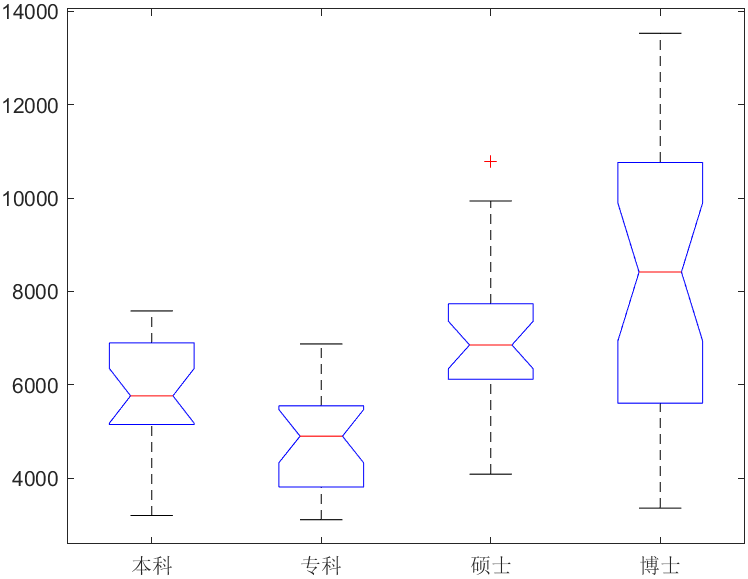
例子2 分析个人受教育程度（定类变量）是否给个人的经济收入（定量变量）带来显著性影响。

多独立样本Kruskal-Wallis检验-SPSSPRO帮助中心

分析个人受教育程度（定类变量）是否给个人的经济收入（定量变量）带来显著性影响

数据：个人受教育程度与个人的经济收入统计.xlsx

Kruskal-Wallis 检验分析结果表

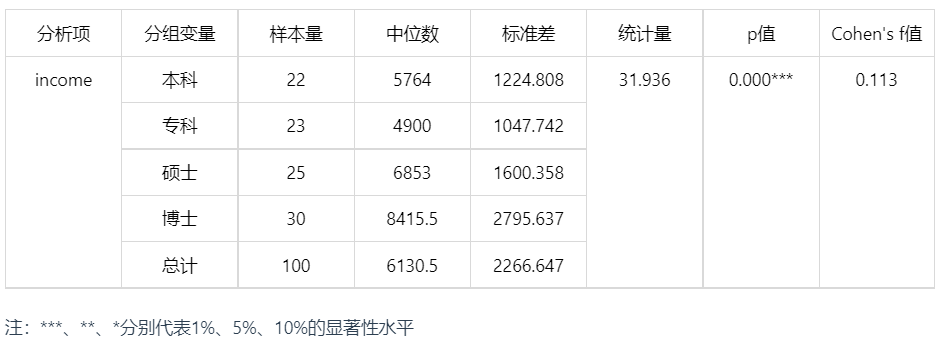
Kruskal-Wallis 检验结果显示，不同教育水平与个人收入的关系，检验结果 p 值为 0(<0.05)，因此统计结果显著，说明不同受教育程度在收入上存在显著差异。

进行事后多重分析

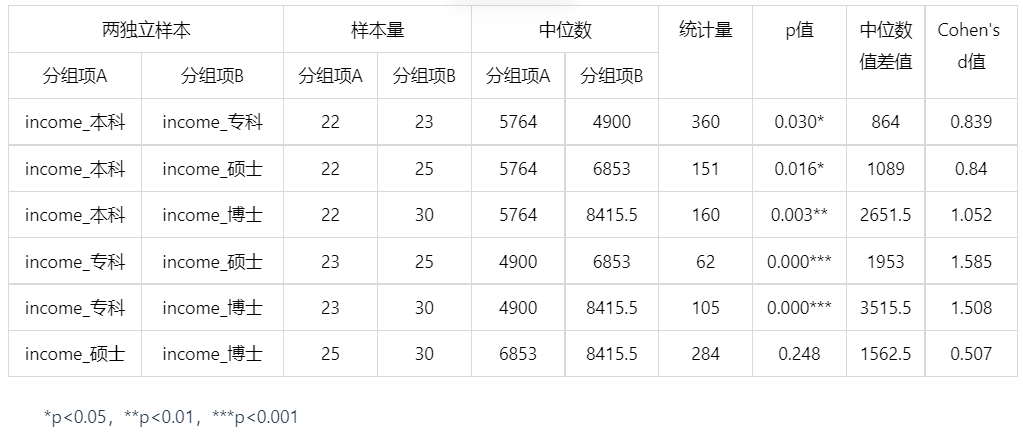
根据以上结果，可知，除去硕博的差异幅度是中等以外，其他的差异幅度都相当的大，可见学历的重要性。

Kruskal-Wallis 检验代码实现

Matlab

文档：Kruskal-Wallis test - MATLAB kruskalwallis - MathWorks 中国

事后多重比较用multicompare提供的"dunn-sidak"方法

关于"dunn-sidak"是不是Dunn检验的讨论

nonparametric - Is Dunn-Sidak approach in MATLAB multcompare identical to so-called Dunn's test? - Cross Validated (stackexchange.com)

结论："dunn-sidak"是Dunn检验进行 “Bonferroni” 多重比较调整的一种变体、

下面文章就用了"dunn-sidak"方法来多重比较

Associating IDH and TERT Mutations in Glioma with Diffusion Anisotropy in Normal-Appearing White Matter - PMC (nih.gov)

Increased adiposity is associated with altered skeletal muscle energetics - PMC (nih.gov)

Classifying Glioblastoma Multiforme Follow-Up Progressive vs. Responsive Forms Using Multi-Parametric MRI Features - PMC (nih.gov)

其他多重比较方法

>> tbl  = readtable("个人受教育程度与个人的经济收入统计.xlsx");
>> [p,tbl,stats] = kruskalwallis(tbl.income,tbl.education)

p =
   5.3989e-07


stats = 

  struct with fields:
       gnames: {4×1 cell}
            n: [22 23 25 30]
       source: 'kruskalwallis'
    meanranks: [42 25.6087 60.8400 67.2000]
         sumt: 0

Python

Kruskal 检验文档：kruskal — SciPy v1.14.1 Manual

Kruskal多重比较：scikit-posthocs

import numpy as np
from scipy.stats import kruskal

# 生成示例数据
group1 = np.random.normal(loc=0, scale=1, size=30)
group2 = np.random.normal(loc=1, scale=1, size=30)
group3 = np.random.normal(loc=2, scale=1, size=30)

# 进行Kruskal-Wallis检验
stat, p_value = kruskal(group1, group2, group3)

print(f'Statistic: {stat}')
print(f'P-value: {p_value}')

# 结果解释
if p_value < 0.05:
    print('各组数据存在显著差异')
else:
    print('各组数据不存在显著差异')

参考资料

多独立样本Kruskal-Wallis检验-SPSSPRO帮助中心
Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
Conover W J. Practical Nonparametric Statistics[M]. 2th ed. New York：John Wiley &Sons，Inc，1980.
张林泉.多独立样本 Kruskal-Wallis 检验的原理及其实证分析[J].苏州科技学院学报(自然科学版),2014,31(01):14-16+38.
Kruskal-Wallis检验_哔哩哔哩_bilibili

本文采用署名-非商业性使用-相同方式共享 4.0 国际许可协议，转载请注明出处。