统计分析丨卡方检验

卡方检验（Chi-Square Test）是一种常用于统计学的假设检验方法，属于非参数检验，主要用于分析分类数据（即离散型数据）。通过检验观察数据和理论期望之间的差异，判断变量之间是否存在显著关联或符合期望。卡方检验主要有以下几种类型：

1. 拟合优度检验（Goodness of Fit Test） ：用于检验观测数据的分布是否与预期分布相符合。例如，检验一个骰子是否公平，可以通过观测各个面出现的频率和期望的均匀分布进行比较。

2. 独立性检验（Test of Independence） ：用于判断两个分类变量是否相互独立。比如，在市场调查中，想要了解年龄与购买偏好是否有关联，可以使用独立性检验来判断这两个变量之间的关系。

卡方检验的计算步骤

使用步骤

1. 建立假设：

   • 原假设 $H_0$ ：变量之间无关联或分布符合期望。
   • 备择假设 $H_1$：变量之间有显著关联或分布不符合期望。

2. 计算卡方统计量：根据数据计算卡方值。

   卡方统计量的计算公式为：

   $$\chi^2 = \sum \frac{(Observed - Expected)^2}{Expected}$$

   此公式也叫做皮尔森卡方检验(Pearson χ² )

3. 确定自由度（Degrees of Freedom, df） ：

   卡方拟合优度检验：自由度=类别数目-1

   卡方独立性检验：自由度= (行数−1)×(列数−1)

4. 查找卡方临界值：

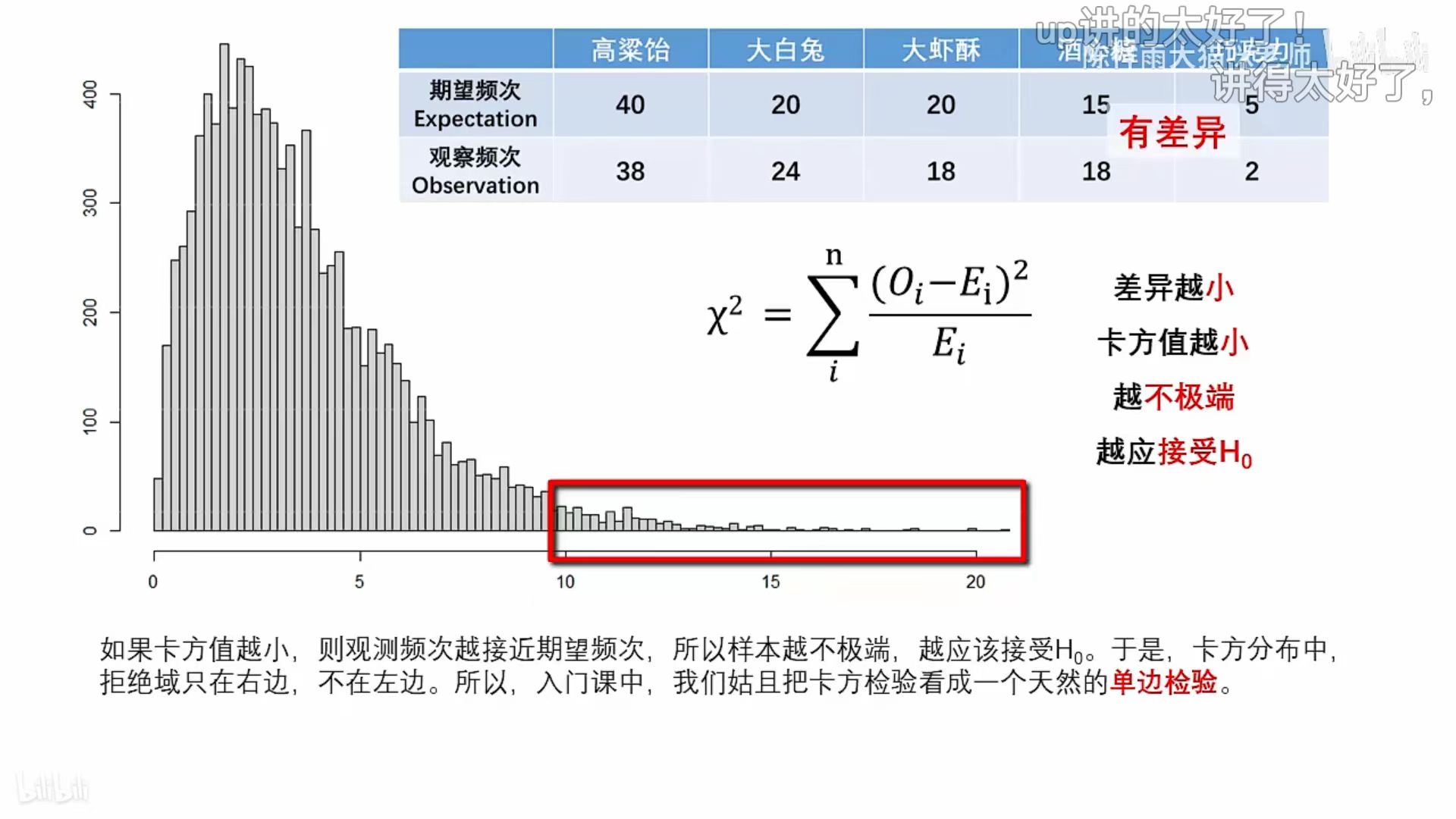
   根据给定的显著性水平（如 0.05）和自由度，查找卡方分布表中的临界值。卡方值越高，“观测数据” 与 “假定无关联的期望数据” 之间差异越大，越可能存在关联关系；卡方值越小，说明“观测数据” 与 “假定无关联的期望数据” 之间差异越大，越可能存在关联关系

5. 做出结论：

   如果计算的卡方值大于临界值，拒绝原假设，认为变量之间存在显著关联；否则，卡方值小于临界值，不拒绝原假设。

计算举例

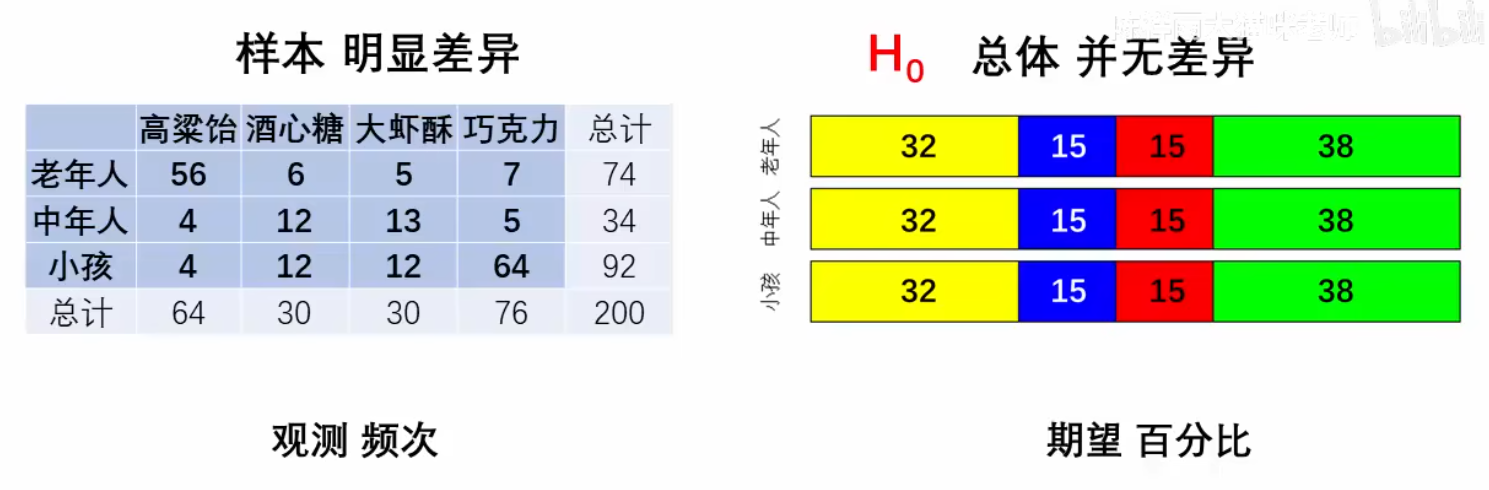
假设在某互联网大厂，员工颈椎疼痛问题很普遍，为了研究 颈椎疼痛 是否与 办公桌类型 相关，公司收集了以下数据：

• 100个员工用传统桌子，其中30个人觉得颈椎疼
• 100个员工用站立桌子，其中10个人觉得颈椎疼

现在，我们使用卡方检验来进行验证

1. 提出假设：

   • 原假设 (H0): 颈椎疼痛与办公桌类型无关（独立）。
   • 备择假设 (H1): 颈椎疼痛与办公桌类型相关（不独立）。

2. 收集数据，并画出如上页的表格

3. 计算卡方值，根据数据我们计算出 χ² = 12.5

   • 计算期望频数

     办公桌类型	颈椎疼痛	无颈椎疼痛
     传统桌	40/200*100 = 20	160/200*100 = 80
     站立桌	40/200*100 = 20	160/200*100 = 80

   • 计算卡方统计量

     $$\chi^2 = \frac{(30 - 20)^2}{20} + \frac{(70 - 80)^2}{80} + \frac{(10 - 20)^2}{20} + \frac{(90 - 80)^2}{80} = 5 + 1.25 + 5 + 1.25 = 12.5$$

4. 查找卡方临界值：

   1. 自由度为 (2-1)*(2-1) = 1
   2. 显著水平为0.05，自由度为1的卡方分布表中的临界值为3.841

5. 做出结论

   χ² = 12.5 > 3.841，卡方值大于临界值，说明p < 0.05，因此，我们可以拒绝零假设，认为办公桌类型和颈椎疼痛之间存在显著的关联、两者并不独立。

卡方检验限制条件

1. 样本量≥40，且理论频数T≥5时用卡方检验的基本公式

   $$\chi^2 = \sum \frac{(O - E)^2}{E}$$

2. 样本量≥40，但理论频数1≤T<5时用卡方检验校正公式；

   美国统计学家F. Yates在1934年提出了一个计算卡方值的连续性校正公式

   $$\chi^2 = \sum \frac{(|O - E| - 0.5)^2}{E}$$

   其中，$O$ 是观测频数，$E$ 是期望频数，$0.5$ 是校正因子。这一校正减少了卡方统计量的值，降低了检验的偏向性，减少了假阳性结果的概率。

3. 若样本量<40或理论频数T<1时，需改用Fisher精确检验法进行统计分析。

概念笔记

• 卡方检验的p值意义

  • 意义：原假设为真的情况下，观测到当前数据（卡方值）或更极端数据（更大的卡方值）的概率

• 怎么通过生成模拟数据计算p值

  办公桌类型	颈椎疼痛	无颈椎疼痛	总计
  传统桌	30	70	100
  站立桌	10	90	100
  总计	40	160	200

  • 原假设 (H0): 颈椎疼痛与办公桌类型无关（独立）。
  • 备择假设 (H1): 颈椎疼痛与办公桌类型相关（不独立）。

  根据期望频率，符合零假设的总体，总共20000个样本

  办公桌类型	颈椎疼痛	无颈椎疼痛
  传统桌	2000	8000
  站立桌	2000	8000

  然后抽样200个样本，计算卡方值，抽样10000次，得到模拟出的卡方分布，并与实际的卡方分布做比较，查看两种方法计算的pvalue差别

  具体代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56

  % 定义各类人群与糖果的偏好数量 % 创建 population 数据 population = [... repmat("传统桌-颈椎疼痛", 2000, 1); ... repmat("传统桌-无颈椎疼痛", 8000, 1); ... repmat("站立桌-颈椎疼痛", 2000, 1); ... repmat("站立桌-无颈椎疼痛", 8000, 1); ... ]; % 获取 population 的总长度 n = length(population); % 对 population 进行重排 shuffled_population = population(randperm(n)); % 定义人群类别 categories = ["传统桌-颈椎疼痛", "传统桌-无颈椎疼痛", "站立桌-颈椎疼痛", "站立桌-无颈椎疼痛"]; % 定义抽样大小 sample_size = 200; % 定义重复抽样次数 num_iterations = 10000; % 存储每次抽样的卡方值 chi2_values = zeros(num_iterations, 1); % 重复抽样并计算卡方值 for i = 1:num_iterations % 从样本中随机抽取200个数据 sampled_population = datasample(shuffled_population, sample_size, 'Replace', false); % 计算每类人群在抽样中的观测频率 observed = [... sum(sampled_population == "传统桌-颈椎疼痛"),sum(sampled_population == "传统桌-无颈椎疼痛"); sum(sampled_population == "站立桌-颈椎疼痛"),sum(sampled_population == "站立桌-无颈椎疼痛"); ]; % 计算期望频数（注意，这里的期望频数需要每次抽样单独算，不能直接用总体的期望频数来算，不然就成卡方拟合优度检验了） row_sums = sum(observed, 2); col_sums = sum(observed, 1); expected = row_sums / sample_size * col_sums; % 计算卡方值 chi2_values(i) = sum(sum((observed - expected).^2 ./ expected)); end % 绘制卡方统计量的分布直方图 figure; histogram(chi2_values, 'Normalization', 'pdf'); hold on; plot(x, chi2pdf(x, 1), 'r-', 'LineWidth', 2); legend('模拟分布', '理论\chi^2(1)分布'); xlabel('卡方值'); ylabel('概率密度'); title('模拟与理论卡方分布比较'); % 计算p值 p_value = mean(chi2_values >= 12.5); fprintf('模拟p值: %.4f\n', p_value);

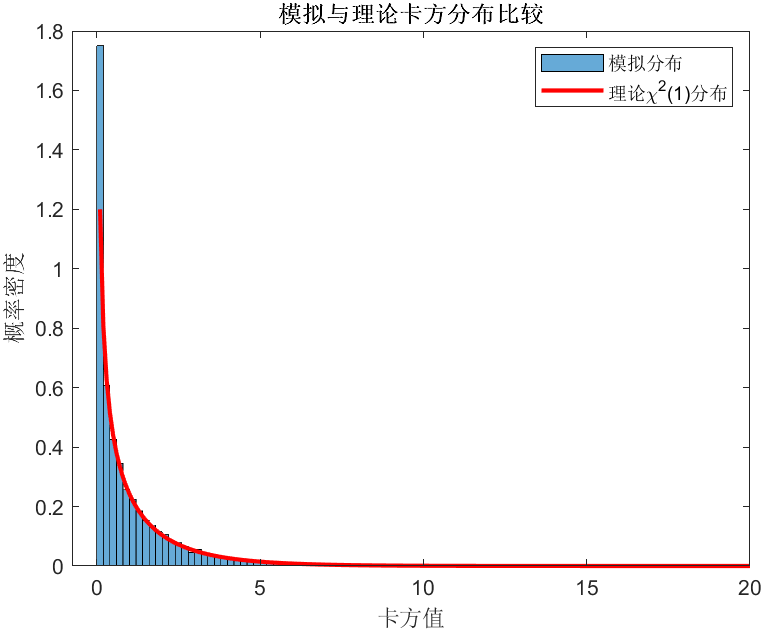
模拟分布计算的计算pvalue

1
2
3

>> pvalue = mean(chi2_values >= 12.5)

0.0004

用卡方的累计分布计算pvalue： p-value = 1- p_CDF

1
2
3
4
5
6
7
8

% 自由度
df = 1;
% 卡方统计量
chi2_stat = 12.5;
% 计算p值
p_value = 1 - chi2cdf(chi2_stat, df);
% 输出p值
disp(p_value); % 结果：4.0695e-04

可以看到，生成大量样本计算的pvlaue结果和公式计算的结果是比较相近的

• 卡方检验的自由度（Degrees of Freedom, df）

  • 卡方拟合优度检验：自由度=类别数目-1
  • 卡方独立性检验：自由度= (行数−1)×(列数−1)

• 卡方统计量的值与可能性的关系

  • 卡方统计量越大，代表越极端，出现可能越小。所以，如果计算的卡方值大于临界值，拒绝原假设，认为变量之间存在显著关联；否则，卡方值小于临界值，不拒绝原假设。

• 卡方检验是单侧检验吗？

  卡方检验是单侧的，只关心偏差的大小，而不关心偏差的方向。

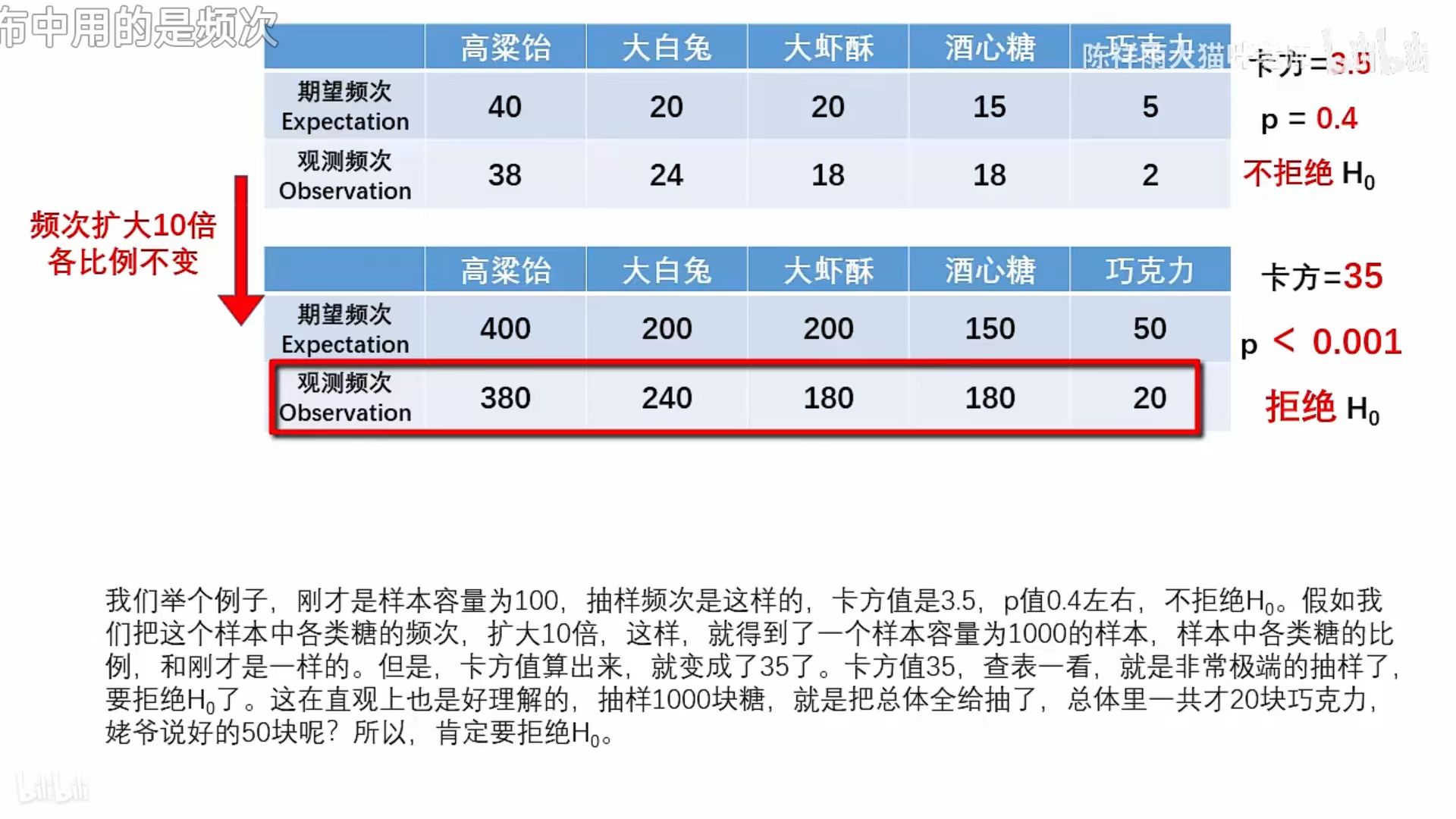
• 卡方检验用的是频数而不是频率

• 卡方分布函数

  • 概率密度函数（PDF）：自由度越高，函数越扁

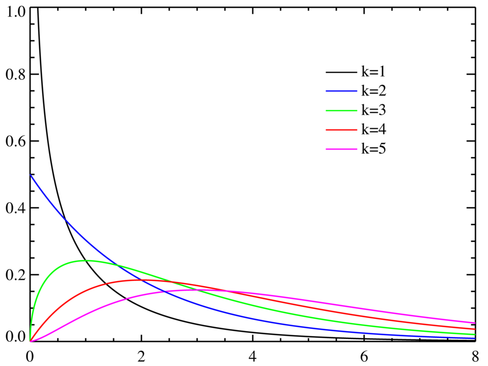
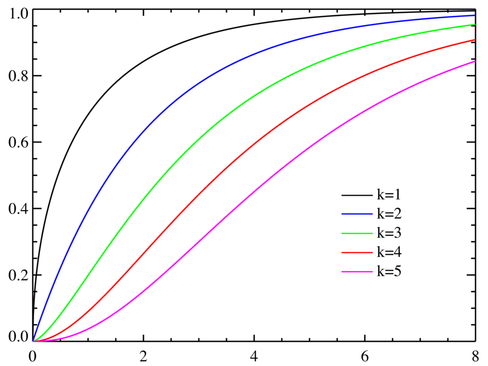
• 累积分布函数（CDF）

  卡方分布的累积分布函数为：

Matlab 实现卡方检验

使用chi2test包：chi2test - File Exchange - MATLAB Central (mathworks.cn)

1
2
3
4
5
6
7
8
9
10
11
12
13
14

>> tbl

tbl =

    30    70
    10    90
>> [p,Q] =chi2test(tbl)
p =

   4.0695e-04

Q =

   12.5000

chi2test代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

function [p, Q]= chi2test(x)
	% Check the arguments.
	if(nargin ~= 1),			error('One and only one argument required!');					end
	if(ndims(x) ~= 2),			error('The argument (x) must be a 2d matrix!');					end
	if(any(size(x) == 1)),		error('The argument (x) must be a 2d matrix!');					end
	if(any(~isreal(x))),		error('All values of the argument (x) must be real values!');	end

	% Calculate Q = sum( (a-np*)^2/(np*(1-p*)) )
	s=		size(x, 1);
	r=		size(x, 2);
	np=		sum(x, 2)/sum(sum(x)) * sum(x);		% p=sum(x, 2)/sum(sum(x)) and n=sum(x)
	Q=		sum(sum((x-np).^2./(np)));

	% Calculate cdf of chi-squared to Q. Degrees of freedom, v, is (r-1)*(s-1).
	p=		1 - chi2cdf(Q,(r-1)*(s-1));
end

参考

• 什么是卡方检验

  • 通俗统计学原理入门22 卡方拟合优度检验 卡方检验 Chi-Square Test for Goodness of Fit 谁动了姥爷的什锦糖_哔哩哔哩_bilibili
  • 通俗统计学原理入门23 卡方独立性检验的基本原理 Chi Square Test of Independence_哔哩哔哩_bilibili
  • 终于有人把卡方检验讲明白了！！！ - 小红书 (xiaohongshu.com)

• matlab 实现卡方检验：

  • How can I perform a chi-square test to determine how statistically different two proportions are in Statistics Toolbox 7.2 (R… - MATLAB Answers - MATLAB Central (mathworks.cn)：介绍了三种方法，用crosstab、chi2cdf、chi2gof函数计算卡方检验
  • chi2test - File Exchange - MATLAB Central (mathworks.cn)：直接输入列联表就可以计算卡方检验的结果

‍