主成分分析是一种常用的数据降维方法，它利用正交变换把由线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据，这些线性无关的变量被称为主成分。

主成分分析计算指标权重用于对象综合评价的原理是能对信息进行压缩，把多个指标变换成几个综合指标，从而计算得到指标的权重和对象的综合得分。

为了计算指标的权重，将**PCA得到的特征向量当作指标在主成分中的“贡献系数**”，用来描述每个主成分对各个指标的依赖程度，将**各个主成分的累计方差贡献率**当作主成分的重要性权重，每个指标在不同主成分的特征向量值相乘主成分累计方差贡献率并加和即为对象的综合得分。

为了计算对象的综合得分，将PCA降维后的数据（主成分得分）当做是综合指标得分，将**各个主成分的累计方差贡献率**当作是主成分重要性权重，主成分得分相乘对应累计方差贡献率并加和即为对象的综合得分。

目录

  1. 主成分分析计算步骤

    1. 准备原始矩阵 X
    2. 计算正向化矩阵 X′
    3. KMO和Barlette检验
    4. 计算标准化矩阵 Z
    5. 计算协方差矩阵 R
    6. 计算特征值 λ\lambda 和特征向量 uu
    7. 计算主成分的方差贡献率和累计方差贡献率
    8. 根据一定的原则确定主成分数量 k
    9. 计算主成分系数/因子载荷
    10. 计算主成分得分
    11. 计算前 k
    12. 计算指标权重
    13. 计算对象综合得分

  2. 代码实现

    1. matlab实现
    2. python实现

  3. 相关考试题目

  4. 参考

主成分分析计算步骤

主成分分析计算权重以及综合评价的步骤如下：

1. 准备原始矩阵 XX

假设有 nn 个对象，pp 个指标，则原始数据矩阵为 n×pn \times p 的矩阵：

X=[x11x12⋯x1px21x22⋯x2p⋮⋮⋱⋮xn1xn2⋯xnp]X = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{np} \end{bmatrix}

其中，xijx_{ij} 表示第 ii 个对象在第 jj 个指标下的评分数据。

例如

对象 指标1 指标2 指标3
对象1 1 3 1
对象2 2 2 2
对象3 2 1 3
对象4 3 2 1

2. 计算正向化矩阵 X′X'

指标类型一般有三种：

  1. 正向指标，越大越好，如收入；
  2. 负向指标，越小越好，如成本；
  3. 适度指标，在某个范围最好，如水中的PH值，越接近7越好。

根据不同类型的指标，需要进行不同的正向化处理：

  • 正向（极大型）指标： 无需变化

  • 负向（极小型）指标： max(x)−xmax(x) - x

  • 适度指标：

    zij′={1−a−xijmax(a−xjmin,xjmax−b),xij<a1,a≤xij≤b1−xij−bmax(a−xjmin,xjmax−b),xij>bz'_{ij} = \begin{cases} 1 - \frac{a - x_{ij}}{max(a - x_j^{min}, x_j^{max} - b)}, & x_{ij} < a \\ 1, & a \le x_{ij} \le b \\ 1 - \frac{x_{ij} - b}{max(a - x_j^{min}, x_j^{max} - b)}, & x_{ij} > b \end{cases}

    其中 aa 和 bb 不相等时可以叫做范围型指标，aa 和 bb 相等时可以叫做中间型指标。

3. KMO和Barlette检验

KMO检验：用于比较变量间的简单相关系数与偏相关系数

KMO值 是否适合做主成分分析
>0.8 非常适合
0.7~0.8 一般适合
0.6~0.7 不太适合
0.5~0.6 不适合
<0.5 极不适合

Bartlett检验：检验相关系数矩阵是否是单位矩阵

  • 假设

    • 原假设 (H0): 相关系数矩阵为单位矩阵。
    • 备择假设 (H1): 相关系数矩阵不是单位矩阵。

  • 近似卡方值：用于衡量观测到的相关矩阵与单位矩阵之间的差异。

  • 自由度 (df) ：与卡方检验相关的自由度。

  • p值：如果p值小于0.05，则认为变量间存在足够的相关性，可以进行PCA。

4. 计算标准化矩阵 ZZ

主成分分析最常用的标准化方法是 Z-score 标准化，即：

zij=xij′−μjσj(j=1,2,…,p)z_{ij} = \frac{x'_{ij} - \mu_j}{\sigma_j} \quad (j = 1,2,\dots,p)

其中 μj\mu_j 和 σj\sigma_j 分别是正向化矩阵 X′X' 中第 jj 个变量的均值和标准差。

将原数据变为均值为0，标准差为1的数据。

5. 计算协方差矩阵 RR

标准化后的矩阵

对于已标准化的矩阵，我们可以使用以下公式计算其协方差矩阵：

rij=1n−1∑i=kn(zki−ziˉ)(zkj−zjˉ)r_{ij} = \frac{1}{n-1} \sum_{i=k}^{n} (z_{ki} - \bar{z_i})(z_{kj} - \bar{z_j})

其中：

  • rijr_{ij} 表示第 ii 个变量和第 jj 个变量之间的相关系数。
  • nn 表示样本数量。
  • zkiz_{ki} 表示第 kk 个样本的第 ii 个变量的标准化值。
  • ziˉ\bar{z_i} 表示第 ii 个变量的标准化值的均值。

所以没有标准化的数据，是不能直接计算协方差矩阵的

未标准化的矩阵： 直接计算相关系数矩阵：

rij=∑k=1n(zki−ziˉ)(zkj−zjˉ)∑k=1n(zki−ziˉ)2∑k=1n(zkj−zjˉ)2r_{ij} = \frac{\sum_{k=1}^{n} (z_{ki} - \bar{z_i})(z_{kj} - \bar{z_j})}{\sqrt{\sum_{k=1}^{n} (z_{ki} - \bar{z_i})^2 \sum_{k=1}^{n} (z_{kj} - \bar{z_j})^2}}

其中：

  • rijr_{ij} 表示第 ii 个变量和第 jj 个变量之间的相关系数。
  • nn 表示样本数量。
  • zkiz_{ki} 表示第 kk 个样本的第 ii 个变量的值。
  • ziˉ\bar{z_i} 表示第 ii 个变量的均值。

相关系数也叫皮尔逊系数，分子是协方差，分母是标准差之积，相当于直接对原始矩阵计算的协方差进行了标准化。

6. 计算特征值 λ\lambda 和特征向量 uu

对于一个给定的 n 阶方阵 A，如果存在一个非零向量 v⃗\vec{\mathbf{v}} 和一个标量 λ，使得以下等式成立：

Av⃗=λv⃗A\vec{\mathbf{v}}= \lambda\vec{\mathbf{v}}

那么，λ 就被称为矩阵 A 的一个特征值，而 v⃗\vec{\mathbf{v}} 就被称为矩阵 A 对应于特征值 λ 的一个特征向量。

PCA会对协方差矩阵 RR 进行特征分解，得到特征值

λ1≥λ2≥⋯≥λp≥0\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_p \geq 0

和对应的特征向量

v1,v2,⋯ ,vpv_{1}, v_{2}, \cdots, v_{p}

7. 计算主成分的方差贡献率和累计方差贡献率

第 ii 个主成分的方差贡献率定义为：

fi=λi∑j=1pλj(i=1,2,⋯ ,p)f_i = \frac{\lambda_i}{\sum_{j=1}^{p} \lambda_j} \quad (i = 1, 2, \cdots, p)

前 kk 个主成分的累计方差贡献率定义为：

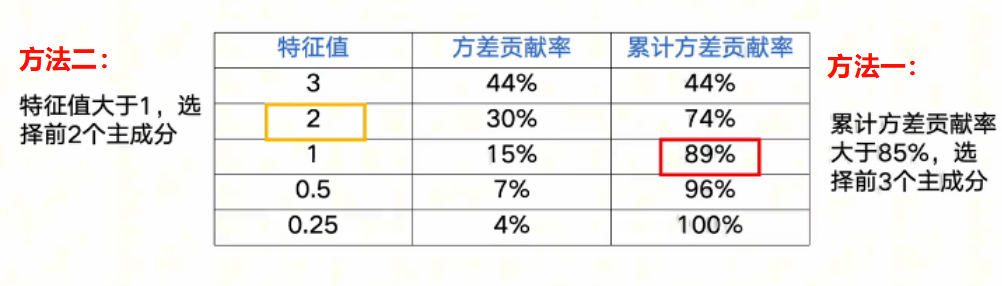
Fk=∑i=1kfi(k=1,2,⋯ ,p)F_k = \sum_{i=1}^{k} f_i \quad (k = 1, 2, \cdots, p)

举例：

特征值 方差贡献率 累计方差贡献率
3 44% 44%
2 30% 74%
1 15% 89%
0.5 7% 96%
0.25 4% 100%

8. 根据一定的原则确定主成分数量 kk

前 kk 个主成分的累计方差贡献率 FkF_k 定义为：

Fk=∑i=1kfi(k=1,2,…,p)F_k = \sum_{i=1}^{k} f_i \quad (k = 1,2,\dots,p)

确定主成分数量 kk 的方法有以下几种，选择其中一种即可，不需要全部使用：

  1. 累计方差贡献率： 选择累计方差贡献率大于某个阈值（例如 85%）时的最小的 kk 个主成分。阈值一般在 80%~90% 之间。
  2. 特征值： 选择特征值大于某个阈值（例如 1）时的最小的 kk 个主成分。
  3. 手动选择： 根据业务经验确定主成分数量。

9. 计算主成分系数/因子载荷

主成分系数就为特征向量

载荷是特征向量乘以对应特征值的平方根，载荷代表每个主成分上各个原始变量的权重系数。

计算公式为：

lij=λjvij(i=1,2,…,p;j=1,2,…,p)l_{ij}= \sqrt{\lambda_{j}}v_{ij}\quad (i = 1,2,\dots,p; j = 1,2,\dots,p)

10. 计算主成分得分

主成分得分即主成分分析对数据进行处理后，得到的数据在特征空间的投影。

在Python和Matlab中，可以直接通过调用函数得到，不需要手动计算。

手动计算的公式：主成分得分=标准化数据矩阵Z×特征向量矩阵A

如果我们选择了 kk 个主成分，则只需要计算对象在这 kk 个主成分上的得分即可。第 ii 个对象在第 jj 个主成分下的得分：

sij=aj1zi1+aj2zi2+⋯+ajpzip=∑k=1pajkziks_{ij}= a_{j1}z_{i1}+ a_{j2}z_{i2}+ \dots + a_{jp}z_{ip}= \sum_{k=1}^{p}a_{jk}z_{ik}

例子：

标准化矩阵Z:

对象 指标1 指标2 指标3 指标4 指标5
A 0.1 0.2 0.3 0.4 0.5
B … … … … …
C … … … … …
D … … … … …
E … … … … …
F … … … … …
G … … … … …

前3个主成分的主成分系数(特征向量)矩阵A:

指标 主成分1 主成分2 主成分3
指标1 0.1 … …
指标2 0.2 … …
指标3 0.3 … …
指标4 0.4 … …
指标5 0.5 … …

s=0.1x0.1+0.2x0.2+0.3x0.3+0.4x0.4+0.5x0.5

11. 计算前 kk 个主成分的权重

基于方差贡献率占前 kk 个主成分方差贡献率之和的比值得到权重：

wi=fi∑j=1kfj(i=1,2,…,k)w_{i} = \frac{f_{i}}{\sum_{j=1}^{k}f_{j}}\quad (i = 1, 2, \ldots, k)

其中 fif_i 是第 ii 个主成分的方差贡献率。

例子：主成分分析结果

特征值 方差贡献率 累计方差贡献率
3 44% 44%
2 30% 74%
1 15% 89%
0.5 7% 96%
0.25 4% 100%

主成分的权重计算（只选择前3个主成分）

  • 第一主成分：4444+30+15=0.49\frac{44}{44+30+15}= 0.49
  • 第二主成分：3044+30+15=0.34\frac{30}{44+30+15} = 0.34
  • 第三主成分：1544+30+15=0.17\frac{15}{44+30+15} = 0.17

12. 计算指标权重

注意： 一般情况下主成分分析计算权重和计算综合得分是两种方法，根据你的需要写入论文，即你用主成分分析计算指标权重就使用第 12 步的公式，使用主成分分析计算综合得分就使用第 13 步的公式。（不过我觉得有指标权重可以更好解释对象综合得分的结果）

指标权重=主成分权重与主成分系数（特征向量）对应相乘求和

公式：

Si=∑j=1kwjaij(i=1,2,⋯ ,p)S_{i} = \sum_{j=1}^{k}w_{j} a_{ij}\quad (i = 1, 2, \cdots, p)

对指标的综合得分归一化，得到指标权重：

Wi=Si∑i=1pSiW_i = \frac{S_i}{\sum_{i=1}^{p} S_i}

例子：

指标 主成分1 主成分2 主成分3
指标1 0.3 0.2 0.1
指标2 … … …
指标3 … … …
指标4 … … …
指标5 … … …

第1、2、3主成分的权重分别为：0.49、0.34、0.17，则指标1的综合得分系数为：

0.49×0.3+0.34×0.2+0.17×0.10.49 \times 0.3 + 0.34 \times 0.2 + 0.17 \times 0.1

计算出所有指标的综合得分系数之后，归一化得到指标权重：

Wi=Si∑i=1pSiW_i = \frac{S_i}{\sum_{i=1}^{p} S_i}

13. 计算对象综合得分

对象综合得分=主成分权重与主成分得分对应相乘求和

公式：

Si=∑j=1kwjsijS_i = \sum_{j=1}^{k} w_{j} s_{ij}

例子：

假设对象A在主成分1、2、3下的得分分别为0.3、0.2、0.1，主成分1、2、3的权重分别为0.49, 0.34, 0.17‾\underline{}，则对象A的综合得分为：

0.49×0.3+0.34×0.2+0.17×0.1=0.2320.49 \times 0.3 + 0.34 \times 0.2 + 0.17 \times 0.1 = 0.232

最终对象综合得分和排序表示如下：

对象 主成分1得分 主成分2得分 主成分3得分 综合得分 排序
A 0.3 0.2 0.1 0.232 1
B … … … 0.22 2
C … … … 0.21 3
D … … … 0.20 4
E … … … 0.19 5
F … … … 0.18 6
G … … … 0.17 7

代码实现

示例数据：主成分分析示例文件.xlsx

来自：主成分分析法计算指标权重和对象评价，步骤介绍和软件演示_哔哩哔哩_bilibili

输出结果

matlab实现

代码功能

  • 支持三种方法选择主成分个数

    • 根据特征值
    • 根据累计方差贡献率
    • 手动设置主成分个数

  • 输出

    • KMO 和 Bartlett 检验表：包含 “KMO 值”“Bartlett 球形检验 - 卡方值”“Bartlett 球形检验 - 自由度”“Bartlett 球形检验 - p 值” 等行名对应的检验结果数据，详细记录了数据适用性检验的各项指标情况。
    • 标准化矩阵表：展示经过 Z-Score 标准化处理后的数据，包含样本名（若有读取行名）以及各变量对应的标准化数值，用于后续查看数据标准化后的状态。
    • 相关系数矩阵表：呈现数据标准化后的相关系数矩阵，行列名与原数据变量名一致（添加了合适的表头处理），反映各变量间的相关关系情况。
    • 方差解释表：有 “成分编号”“特征根”“方差解释率 (%)”“累计方差解释率 (%)” 等列，清晰列出各主成分在解释数据方差方面的相关指标，辅助确定主成分的重要性及数量选择等。
    • 载荷系数矩阵表：包含特征名、各主成分（带有方差解释率后缀，如PC1(XX%)）对应的载荷系数以及 “共同度（公因子方差）” 等内容，展示主成分与原始变量间的载荷关系及共同度情况。
    • 特征向量矩表：以特征名为行名，各主成分（带方差解释率后缀）为列名，展示特征向量相关数据，体现主成分分析中特征向量的构成情况。
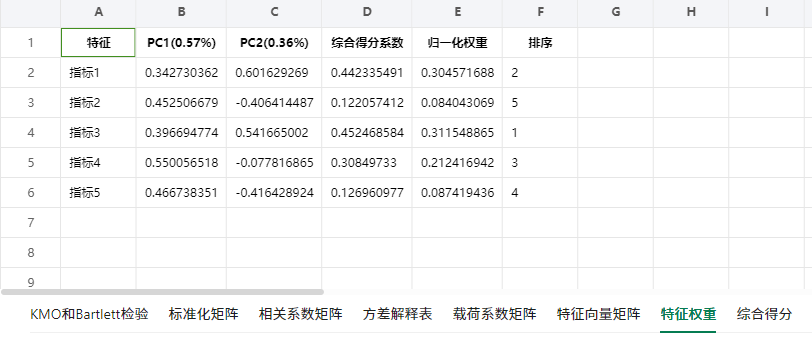
    • 特征权重表：涵盖特征名、各主成分（带方差解释率后缀）对应的相关系数、“综合得分系数”“归一化权重”“排序” 等列，用于呈现各特征在综合评价中的权重相关信息。
    • 综合得分表：展示样本名、各主成分（带方差解释率后缀）的得分、“综合得分” 以及 “排序” 等内容，呈现各样本基于主成分分析得出的综合得分及相应排序情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
pca_analysis("主成分分析示例文件.xlsx", 'isReadRowNames', true, 'method', 'variance', 'threshold', 0.7)


function pca_analysis(filename, opts)
% 函数使用说明
% pca_analysis(filename, opts)
%
% 参数:
%   filename (string): 输入数据文件的路径，支持 Excel 文件格式。
%   opts (struct): 可选参数结构体，包含以下字段：
%       - isReadRowNames (logical): 是否读取行名，默认为 false。
%       - method (string): 确定主成分数量的方法，可选值为 'variance', 'eigenvalue', 'manual'，默认为 'variance'。
%       - threshold (double): 方法对应的阈值，默认为 0.85。
%       - output_filename (string): 输出文件的路径，默认为输入文件名加 '_pca_results.xlsx' 后缀。
%
% 示例:
%   pca_analysis("data.xls", 'isReadRowNames', true, 'method', 'variance', 'threshold', 0.7)
%   pca_analysis("data.xls", 'method', 'eigenvalue', 'threshold', 1.0)
%   pca_analysis("data.xls", 'method', 'manual', 'threshold', 3)
%   pca_analysis("data.xls", 'method', 'manual', 'threshold', 3, 'output_filename', 'results.xlsx')
    arguments
        filename (1, 1) string {mustBeFile}
        opts.isReadRowNames (1, 1) logical = false
        opts.method (1, 1) string {mustBeMember(opts.method, ["variance", "eigenvalue", "manual"])} = "variance"
        opts.threshold (1, 1) double {mustBePositive} = 0.85
        opts.output_filename (1, 1) string = ""
    end

    % 设置输出文件路径
    if opts.output_filename == ""
        [filepath, name, ~] = fileparts(filename);
        opts.output_filename = fullfile(filepath, strcat(name, '_pca_results.xlsx'));
    end

    % 如果输出文件已存在，则删除
    if isfile(opts.output_filename)
        delete(opts.output_filename);
    end

    % --- 1. 导入数据 ---
    tbl = readtable(filename, 'ReadRowNames', opts.isReadRowNames, 'VariableNamingRule', 'preserve');
    data = table2array(tbl);
    [rows, cols] = size(data);

    if ~opts.isReadRowNames
        tbl.Properties.RowNames = arrayfun(@(x) sprintf('%d', x), 1:rows, 'UniformOutput', false);
    end

    fprintf('数据矩阵大小为：%d 行 %d 列\n', rows, cols);

    % --- 2. KMO 和 Bartlett 检验 ---
    % 计算相关系数矩阵
    R = corrcoef(data);

    % 计算偏相关系数矩阵
    R_inv = inv(R);
    partial_corr = -R_inv ./ sqrt(diag(R_inv) * diag(R_inv)');

    % 计算 KMO
    MSA = sum(R .^ 2, 2) - 1; % MSA for each variable
    MSA_partial = sum(partial_corr .^ 2, 2) - 1;
    kmo = sum(MSA) / (sum(MSA) + sum(MSA_partial));

    % Bartlett 球形检验
    [n_samples, n_cols] = size(data);
    chi_square =- (n_samples - 1 - (2 * n_cols + 5) / 6) * log(det(R));
    df = n_cols * (n_cols - 1) / 2;
    p_value = 1 - chi2cdf(chi_square, df);

    % 评估 KMO 值
    if kmo >= 0.8
        kmo_interpretation = '非常适合';
    elseif kmo >= 0.7
        kmo_interpretation = '比较适合';
    elseif kmo >= 0.6
        kmo_interpretation = '可以';
    else
        kmo_interpretation = '不适合';
        warning('KMO值较低，数据可能不适合进行主成分分析！');
    end

    % 评估 Bartlett 检验结果
    if p_value < 0.05
        bartlett_interpretation = '适合';
    else
        bartlett_interpretation = '不适合';
        warning('Bartlett检验p值大于0.05，数据可能不适合进行主成分分析！');
    end

    % 显示检验结果
    fprintf('\n--- KMO 和 Bartlett 检验结果 ---\n');
    fprintf('KMO 值: %.3f (%s进行主成分分析)\n', kmo, kmo_interpretation);
    fprintf('Bartlett 球形检验:\n');
    fprintf('  卡方值: %.3f\n  自由度: %d\n  p值: %.6f (%s进行主成分分析)\n\n', ...
        chi_square, df, p_value, bartlett_interpretation);

    % 将检验结果添加到输出表格
    test_results = array2table({ ...
                                    sprintf('%.3f (%s)', kmo, kmo_interpretation); ...
                                    sprintf('%.3f', chi_square); ...
                                    sprintf('%d', df); ...
                                    sprintf('%.6f (%s)', p_value, bartlett_interpretation)}, ...
        'VariableNames', {'检验结果'}, ...
        'RowNames', {'KMO值', 'Bartlett球形检验-卡方值', ...
           'Bartlett球形检验-自由度', 'Bartlett球形检验-p值'});

    % --- 2. 数据标准化 (Z-Score) ---
    data_standardized = zscore(data);

    % --- 3. 计算相关系数矩阵 ---
    correlation_matrix = corrcoef(data_standardized);

    % --- 4. 执行主成分分析 ---
    [coeff, score, latent, ~, explained, ~] = pca(data_standardized);

    % --- 5. 确定主成分数量 k ---
    variance_ratio = explained / 100;
    cumulative_variance_ratio = cumsum(variance_ratio);

    switch opts.method
        case 'variance'
            num_components = find(cumulative_variance_ratio > opts.threshold, 1, 'first');

            if isempty(num_components)
                num_components = cols;
            end

        case 'eigenvalue'
            num_components = find(latent > opts.threshold, 1, 'last');

            if isempty(num_components)
                num_components = cols;
            end

        case 'manual'
            num_components = opts.threshold;
        otherwise
            error('无效的 method. 请使用 ''variance'', ''eigenvalue'', 或 ''manual''.');
    end

    % --- 6. 计算特征向量矩阵 (载荷系数矩阵) ---
    eigenvector_matrix = coeff(:, 1:num_components);

    % --- 6.1 计算载荷系数矩阵 ---
    loadings = eigenvector_matrix .* sqrt(latent(1:num_components))';

    % --- 6.2 计算共同度 ---
    communality_loadings = sum(loadings .^ 2, 2); % 载荷系数矩阵的共同度

    % --- 6.3 创建载荷系数表 ---
    % **修改部分：添加方差解释率后缀**
    loadings_table_colnames = arrayfun(@(x) sprintf('PC%d(%.1f%%)', x, explained(x)), 1:num_components, 'UniformOutput', false);
    loadings_table = array2table(loadings, ...
        'VariableNames', loadings_table_colnames, ...
        'RowNames', tbl.Properties.VariableNames);
    loadings_table = addvars(loadings_table, communality_loadings, 'After', size(loadings_table, 2), ...
        'NewVariableNames', {'共同度（公因子方差）'});
    loadings_table = addvars(loadings_table, tbl.Properties.VariableNames', 'Before', 1, ...
        'NewVariableNames', {'特征'});

    % --- 6.4 创建特征向量表 ---
    % **修改部分：添加方差解释率后缀**
    eigenvector_table_colnames = arrayfun(@(x) sprintf('PC%d(%.1f%%)', x, explained(x)), 1:num_components, 'UniformOutput', false);
    eigenvector_table = array2table(eigenvector_matrix, ...
        'VariableNames', eigenvector_table_colnames, ...
        'RowNames', tbl.Properties.VariableNames);
    eigenvector_table = addvars(eigenvector_table, tbl.Properties.VariableNames', 'Before', 1, ...
        'NewVariableNames', {'特征'});

    % --- 7. 计算方差解释表 ---
    variance_table = table((1:length(latent))', latent, explained, cumulative_variance_ratio * 100, ...
        'VariableNames', {'成分编号', '特征根', '方差解释率(%)', '累计方差解释率(%)'});

    % --- 8. 绘制碎石图 ---
    figure;
    plot(1:length(latent), latent, '-o', 'LineWidth', 1.5, 'MarkerSize', 6);
    title('碎石图');
    xlabel('主成分');
    ylabel('特征值');
    grid on;
    saveas(gcf, 'scree_plot.png'); % 保存碎石图为 PNG 文件

    % --- 9. 计算特征权重 ---
    variance_ratio_selected = variance_ratio(1:num_components);
    sum_linear_combination = sum(eigenvector_matrix .* variance_ratio_selected', 2);
    composite_score_coeffs = sum_linear_combination / cumulative_variance_ratio(num_components);
    weights = composite_score_coeffs / sum(composite_score_coeffs)';
    [~, sort_weight_idx] = sort(weights, 'descend');
    sort_weight_rank = zeros(size(weights)); % 初始化排名数组

    for k = 1:length(sort_weight_idx)
        sort_weight_rank(sort_weight_idx(k)) = k;
    end

    % --- 10. 计算综合得分 ---
    final_scores = score(:, 1:num_components) * (variance_ratio_selected / cumulative_variance_ratio(num_components));
    [sorted_scores, sort_scores_idx] = sort(final_scores, 'descend');

    % --- 11. 构建特征权重表 ---
    % **修改部分：添加方差解释率后缀**
    weights_table_colnames = arrayfun(@(x) sprintf('PC%d(%.1f%%)', x, explained(x)), 1:num_components, 'UniformOutput', false);
    weights_table = array2table([eigenvector_matrix, composite_score_coeffs, weights, sort_weight_rank], ...
        'VariableNames', [weights_table_colnames, ...
           {'综合得分系数', '归一化权重', '排序'}], ...
        'RowNames', tbl.Properties.VariableNames);
    weights_table = addvars(weights_table, tbl.Properties.VariableNames', 'Before', 1, ...
        'NewVariableNames', {'特征'});

    % --- 12. 构建综合得分表 ---
    score_table_colnames = arrayfun(@(x) sprintf('PC%d(%.1f%%)', x, explained(x)), 1:num_components, 'UniformOutput', false);
    selected_scores = score(:, 1:num_components);
    score_table = array2table([selected_scores(sort_scores_idx, :), sorted_scores, (1:rows)'], ...
        'VariableNames', [score_table_colnames, ...
           {'综合得分', '排序'}], ...
        'RowNames', tbl.Properties.RowNames(sort_scores_idx));
    score_table = addvars(score_table, tbl.Properties.RowNames(sort_scores_idx), 'Before', 1, ...
        'NewVariableNames', {'样本'});

    % --- 13. 输出到 Excel ---
    writetable(test_results, opts.output_filename, 'Sheet', 'KMO和Bartlett检验', 'WriteRowNames', true, 'WriteMode', 'overwrite');

    data_standardized_table = array2table(data_standardized, 'VariableNames', tbl.Properties.VariableNames);
    data_standardized_table = addvars(data_standardized_table, tbl.Properties.RowNames, 'Before', 1, ...
        'NewVariableNames', {'样本'});
    writetable(data_standardized_table, opts.output_filename, 'Sheet', '标准化矩阵');

    % 为相关系数矩阵添加行名和列名
    corr_table = array2table(correlation_matrix, ...
        'VariableNames', tbl.Properties.VariableNames, ...
        'RowNames', tbl.Properties.VariableNames);
    corr_table = addvars(corr_table, tbl.Properties.VariableNames', 'Before', 1, ...
        'NewVariableNames', {' '});
    writetable(corr_table, opts.output_filename, 'Sheet', '相关系数矩阵');

    writetable(variance_table, opts.output_filename, 'Sheet', '方差解释表');

    % 写入载荷系数表
    writetable(loadings_table, opts.output_filename, 'Sheet', '载荷系数矩阵');

    % 写入特征向量表
    writetable(eigenvector_table, opts.output_filename, 'Sheet', '特征向量矩阵');

    writetable(weights_table, opts.output_filename, 'Sheet', ['特征权' ...
                                                  '重']);
    writetable(score_table, opts.output_filename, 'Sheet', '综合得分');

    % --- 14. 显示结果 ---
    disp('--- 主成分分析结果 ---');
    fprintf('保留的主成分个数：%d\n', num_components);
    disp('标准化矩阵：');
    disp(data_standardized_table);
    disp('相关系数矩阵：');
    disp(corr_table);
    disp('方差解释表：');
    disp(variance_table(1:num_components, :));
    disp('特征向量矩阵：');
    disp(eigenvector_table);
    disp('载荷系数矩阵：');
    disp(loadings_table);
    disp('特征权重：');
    disp(weights_table);
    disp('综合得分：');
    disp(score_table);

end

python实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity, calculate_kmo
import matplotlib
from scipy import stats
import os

matplotlib.rcParams["font.sans-serif"] = ["SimHei"]
matplotlib.rcParams["axes.unicode_minus"] = False

def pca_analysis(filename, isReadRowNames=True, method='variance', threshold=0.85, output_filename=None):
    """
    主成分分析函数

    Args:
        filename:  输入 Excel 文件名 (字符串).
        k_method: 主成分数量 k 的设置方法 (字符串, 默认='variance'):
                  'variance' - 累计方差贡献率
                  'eigenvalue' - 特征值
                  'manual' - 手动选择
        k_value:  根据 k_method 设置的值 (默认=0.85):
                  当 k_method 为 'variance' 时, k_value 为累计方差贡献率阈值 (例如 0.85)
                  当 k_method 为 'eigenvalue' 时, k_value 为特征值阈值 (例如 1)
                  当 k_method 为 'manual' 时, k_value 为手动选择的主成分数量
        output_filename: 输出Excel文件名 (字符串, 默认=None)
        isReadRowNames: 是否读取行名 (布尔值, 默认=True)
    """

    # --- 1. 导入数据 ---
    try:
        tbl = pd.read_excel(filename, index_col=0 if isReadRowNames else None)
    except FileNotFoundError:
        print(f"错误：找不到文件 '{filename}'")
        return
    except Exception as e:
        print(f"读取文件 '{filename}' 时发生错误：{e}")
        return

    data = tbl.values
    rows, cols = data.shape
    print(f"数据矩阵大小为：{rows} 行 {cols} 列")

    # --- 2. KMO 和 Bartlett 检验 ---
    # 计算相关系数矩阵
    R = np.corrcoef(data, rowvar=False)

    # KMO 计算

    kmo_all, kmo_model = calculate_kmo(data)

    chi_square_value, p_value = calculate_bartlett_sphericity(data)
    df = cols * (cols - 1) / 2

    # 评估 KMO 值
    if (kmo_model >= 0.8):
        kmo_interpretation = "非常适合"
    elif (kmo_model >= 0.7):
        kmo_interpretation = "比较适合"
    elif (kmo_model >= 0.6):
        kmo_interpretation = "可以"
    else:
        kmo_interpretation = "不适合"
        print("警告：KMO值较低，数据可能不适合进行主成分分析！")

    # 评估 Bartlett 检验结果
    if (p_value < 0.05):
        bartlett_interpretation = "适合"
    else:
        bartlett_interpretation = "不适合"
        print("警告：Bartlett检验p值大于0.05，数据可能不适合进行主成分分析！")

    # 显示检验结果
    print("\n--- KMO 和 Bartlett 检验结果 ---")
    print(f"KMO 值: {kmo_model:.3f} ({kmo_interpretation}进行主成分分析)")
    print("Bartlett 球形检验:")
    print(f"  卡方值: {chi_square_value:.3f}")
    print(f"  自由度: {df:.0f}")
    print(f"  p值: {p_value:.6f} ({bartlett_interpretation}进行主成分分析)\n")

    # 将检验结果添加到输出表格
    test_results = pd.DataFrame(
        {
            "检验结果": [
                f"{kmo_model:.3f} ({kmo_interpretation})",
                f"{chi_square_value:.3f}",
                f"{df:.0f}",
                f"{p_value:.6f} ({bartlett_interpretation})",
            ]
        },
        index=["KMO值", "Bartlett球形检验-卡方值", "Bartlett球形检验-自由度", "Bartlett球形检验-p值"],
    )

    # --- 2. 数据标准化 (Z-Score) ---
    data_standardized = (data - np.mean(data, axis=0)) / np.std(data, axis=0, ddof=1)

    # --- 3. 计算相关系数矩阵 ---
    correlation_matrix = np.corrcoef(data_standardized, rowvar=False)

    # --- 4. 执行主成分分析 ---
    pca = PCA()
    pca.fit(data_standardized)

    # 获取特征值和方差解释率
    latent = pca.explained_variance_  # 特征值
    explained = pca.explained_variance_ratio_  # 方差解释率
    cumulative_variance_ratio = np.cumsum(explained)

    # 确定主成分数量
    if (method == "variance"):
        num_components = np.argmax(cumulative_variance_ratio > threshold) + 1
        if (num_components == 0):
            num_components = cols
    elif (method == "eigenvalue"):
        num_components = np.argmax(latent <= threshold)
        if (num_components == 0):
            num_components = cols
    elif (method == "manual"):
        num_components = int(threshold)
    else:
        raise ValueError("无效的 k_method. 请使用 'variance', 'eigenvalue', 或 'manual'.")

    # 重新拟合PCA与选定的组件数
    pca = PCA(n_components=num_components)
    pca.fit(data_standardized)

    # 计算特征向量矩阵
    coeff = pca.components_.T
    # 计算得分
    score = pca.transform(data_standardized)

    # --- 6.1 计算载荷系数矩阵 ---
    loadings = coeff * np.sqrt(pca.explained_variance_)
    # --- 6.2 计算共同度 ---
    communality_loadings = np.sum(loadings**2, axis=1)

    # --- 6.3 创建载荷系数表 ---
    loadings_table_colnames = [f"PC{i}({explained[i-1]:.2f}%)" for i in range(1, num_components + 1)]
    loadings_table = pd.DataFrame(
        loadings,
        columns=loadings_table_colnames,
        index=tbl.columns,  # 修改这里：使用列名作为index
    )
    loadings_table["共同度（公因子方差）"] = communality_loadings
    loadings_table.insert(0, "特征", loadings_table.index)

    # --- 6.4 创建特征向量表 ---
    eigenvector_table_colnames = [f"PC{i}({explained[i-1]:.2f}%)" for i in range(1, num_components + 1)]
    eigenvector_table = pd.DataFrame(
        coeff,
        columns=eigenvector_table_colnames,
        index=tbl.columns, 
    )
    eigenvector_table.insert(0, "特征", eigenvector_table.index)

    # --- 7. 计算方差解释表 ---
    variance_table = pd.DataFrame(
        {
            "成分编号": range(1, len(latent) + 1),
            "特征根": latent,
            "方差解释率(%)": explained * 100,
            "累计方差解释率(%)": cumulative_variance_ratio * 100,
        }
    )

    # --- 8. 绘制碎石图 ---
    plt.figure()
    plt.plot(range(1, len(latent) + 1), latent, "-o", linewidth=1.5, markersize=6)
    plt.title("碎石图")
    plt.xlabel("主成分")
    plt.ylabel("特征值")
    plt.grid(True)
  
    # 获取输入文件所在目录
    input_dir = os.path.dirname(filename)
    plt.savefig(os.path.join(input_dir, "scree_plot.png"))  # 保存碎石图到输入文件目录

    # --- 9. 计算特征权重 ---
    variance_ratio_selected = explained[:num_components]
    sum_linear_combination = np.sum(
        coeff * variance_ratio_selected, axis=1
    )
    composite_score_coeffs = (
        sum_linear_combination / cumulative_variance_ratio[num_components - 1]
    )
    weights = composite_score_coeffs / np.sum(composite_score_coeffs)
    sort_weight_idx = np.argsort(weights)[::-1]
    sort_weight_rank = np.zeros_like(weights, dtype=int)  # 初始化排名数组

    for k in range(len(sort_weight_idx)):
        sort_weight_rank[sort_weight_idx[k]] = k + 1

    # --- 10. 计算综合得分 ---
    final_scores = np.dot(
        score, variance_ratio_selected / cumulative_variance_ratio[num_components - 1]
    )
    sorted_scores = np.sort(final_scores)[::-1]
    sort_scores_idx = np.argsort(final_scores)[::-1]

    # --- 11. 构建特征权重表 ---
    weights_table_colnames = [
        f"PC{i}({explained[i-1]:.2f}%)" for i in range(1, num_components + 1)
    ]
    weights_table = pd.DataFrame(
        np.column_stack(
            [coeff, composite_score_coeffs, weights, sort_weight_rank]
        ),
        columns=weights_table_colnames
        + ["综合得分系数", "归一化权重", "排序"],
        index=tbl.columns,
    )
    weights_table.insert(0, "特征", weights_table.index)

    # --- 12. 构建综合得分表 ---
    score_table_colnames = [
        f"PC{i}({explained[i-1]:.2f}%)" for i in range(1, num_components + 1)
    ]
    score_table = pd.DataFrame(
        np.column_stack(
            [score[sort_scores_idx,:], sorted_scores, np.arange(1, rows + 1)]
        ),
        columns=score_table_colnames + ["综合得分", "排序"],
        index=tbl.index[sort_scores_idx],
    )
    score_table.insert(0, "样本", score_table.index)

    # --- 13. 输出到 Excel ---
    if (output_filename is None):
        base_filename = os.path.splitext(os.path.basename(filename))[0]
        output_filename = f"{base_filename}_pca_results.xlsx"
  
    # 确保输出文件保存在输入文件的目录下
    output_path = os.path.join(input_dir, output_filename)
  
    with pd.ExcelWriter(output_path, engine="openpyxl") as writer:
        test_results.to_excel(writer, sheet_name="KMO和Bartlett检验")

        data_standardized_table = pd.DataFrame(
            data_standardized, columns=tbl.columns, index=tbl.index
        )
        data_standardized_table.insert(0, "样本", data_standardized_table.index)
        data_standardized_table.to_excel(writer, sheet_name="标准化矩阵",index=False)

        corr_table = pd.DataFrame(
            correlation_matrix, columns=tbl.columns, index=tbl.columns
        )
        corr_table.insert(0, " ", corr_table.index)
        corr_table.to_excel(writer, sheet_name="相关系数矩阵",index=False)

        variance_table.to_excel(writer, sheet_name="方差解释表", index=False)
        loadings_table.to_excel(writer, sheet_name="载荷系数矩阵", index=False)
        eigenvector_table.to_excel(writer, sheet_name="特征向量矩阵", index=False)
        weights_table.to_excel(writer, sheet_name="特征权重", index=False)
        score_table.to_excel(writer, sheet_name="综合得分", index=False)

    # --- 14. 显示结果 ---
    print("--- 主成分分析结果 ---")
    print(f"保留的主成分个数：{num_components}")
    print("标准化矩阵：")
    print(data_standardized_table)
    print("相关系数矩阵：")
    print(corr_table)
    print("方差解释表：")
    print(variance_table.iloc[:num_components])
    print("特征向量矩阵：")
    print(eigenvector_table)
    print("载荷系数矩阵：")
    print(loadings_table)
    print("特征权重：")
    print(weights_table)
    print("综合得分：")
    print(score_table)


def main():
    pca_analysis(r"主成分分析示例文件.xlsx", isReadRowNames=True)  # 使用默认参数

if __name__ == "__main__":
    main()

相关考试题目

f(x)=a1x1+a2x2+a3x3+a4x4+a5x5f(x) = a_1 x_1 + a_2 x_2 + a_3 x_3 + a_4 x_4 + a_5 x_5

降维后两个主成分线性关系为

F1=A1x1+A2x2+A3x3+A4x4+A5x5F_1 = A_1 x_1 + A_2 x_2 + A_3 x_3 + A_4 x_4 + A_5 x_5

F2=B1x1+B2x2+B3x3+B4x4+B5x5F_2 = B_1 x_1 + B_2 x_2 + B_3 x_3 + B_4 x_4 + B_5 x_5

F1F_1 方差贡献率为 mm，F2F_2 方差贡献率为 nn，请通过主成分分析确定 a1,a2,a3,a4,a5a_1, a_2, a_3, a_4, a_5 的值，结果用含字母表达式表示，不需要归一化处理。

‍

解答：

某个变量在综合得分模型中的系数 = (该变量在第一主成分中的系数 ***** 第一主成分的方差贡献率 + 该变量在第二主成分中的系数 ***** 第二主成分的方差贡献率) / (第一主成分的方差贡献率 + 第二主成分的方差贡献率)

将这个逻辑应用到我们的问题中，我们可以得到以下公式（由于不需要归一化）：

a1=A1m+B1nm+na_1 = \frac{A_1 m + B_1 n}{m + n}

a2=A2m+B2nm+na_2 = \frac{A_2 m + B_2 n}{m + n}

a3=A3m+B3nm+na_3 = \frac{A_3 m + B_3 n}{m + n}

a4=A4m+B4nm+na_4 = \frac{A_4 m + B_4 n}{m + n}

a5=A5m+B5nm+na_5 = \frac{A_5 m + B_5 n}{m + n}

参考

许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

快来参与讨论吧~