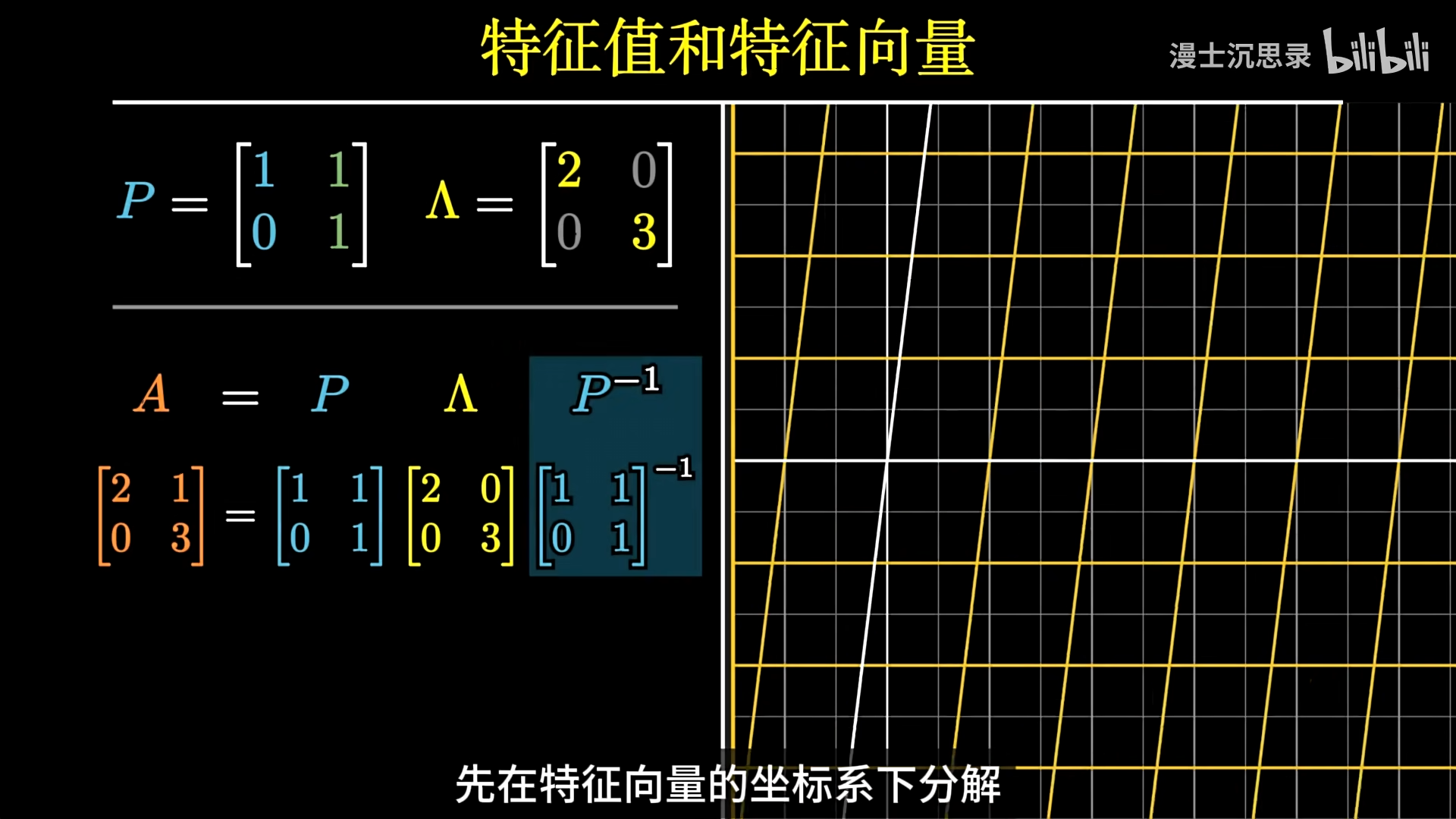
对于一个方阵 A \mathbf{A} A v ⃗ \vec{\mathbf{v}} v λ \lambda λ A v ⃗ = λ v ⃗ \mathbf{A}\vec{\mathbf{v}}= \lambda\vec{\mathbf{v}} A v = λ v λ \lambda λ A \mathbf{A} A (Eigenvalues) ,v ⃗ \vec{\mathbf{v}} v 特征向量(Eigenvectors) 。
但特征值和特征向量的意义和价值不止如此。
在几何意义上,矩阵乘以一个向量,可以看作矩阵对向量所在空间的变换(旋转、拉伸等操作)。而矩阵的特征向量和特征值则直接描述了线性变换的性质。特征向量指明了特定变换下的方向,特征值体现伸缩程度。
特征分解(Eigendecomposition)是将矩阵表示为其特征向量和特征值的组合,即 A = P Λ P − 1 \mathbf{A}= \mathbf{P}\mathbf{Λ}\mathbf{P}^{-1} A = P Λ P − 1 P \mathbf{P} P Λ \mathbf{Λ} Λ 先将向量转换到特征向量定义的坐标系下,特征向量就是这个新坐标系的基底,然后在各个特征向量方向上进行缩放,最后再转换回原始坐标系 。
特征分解不仅能简化计算,比如在复杂运算中可降低难度,而且在主成分分析(PCA)里有着关键应用。在PCA中,特征值 表示了数据在对应特征向量方向上的方差大小 。特征向量代表了数据的主成分方向,即特征空间的基向量 。降维过程就是 通过选择最大特征值对应的特征向量 ,将数据投影到一个较低维度的空间中。
在层次分析法中,利用完全一致的判断矩阵的特殊性质,特征向量归一化后被当做准则层的权重(各个准则的相对重要性),层次分析法算特征向量时可以使用简单的几何平均法和算术平均法算特征向量,最大特征值则用来计算判断矩阵的一致性比率。
本篇笔记会详细介绍特征值和特征向量的定义、意义、计算方法。
笔记目录
特征值和特征向量的定义
特征值和特征向量的意义
特征值和特征向量计算步骤:
特征值和特征向量计算的求解例子
定义:
对于一个给定的 n 阶方阵 A,如果存在一个非零 向量 v ⃗ \vec{\mathbf{v}} v
A v ⃗ = λ v ⃗ A\vec{\mathbf{v}}= \lambda\vec{\mathbf{v}}
A v = λ v
那么,λ 就被称为矩阵 A 的一个特征值 ,而 v ⃗ \vec{\mathbf{v}} v 特征向量 。
这部分学习了
特征向量和特征值的几何意义 矩阵与线性变换的关系:
一个 m × n m \times n m × n A \mathbf{A} A n n n m m m A \mathbf{A} A v ⃗ \vec{\mathbf{v}} v n × 1 n \times 1 n × 1 A v ⃗ \mathbf{A}\vec{\mathbf{v}} A v v ⃗ \vec{\mathbf{v}} v m × 1 m \times 1 m × 1 A v ⃗ \mathbf{A}\vec{\mathbf{v}} A v
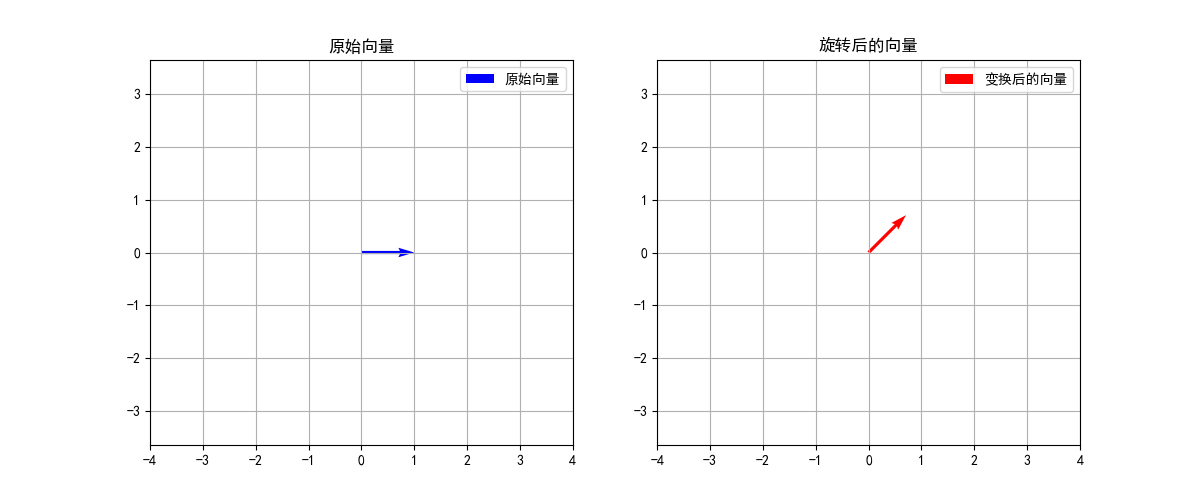
假设我们要将一个二维向量逆时针旋转45度(π/4弧度),这个线性变换可以用以下矩阵表示:
A = [ cos ( 45 ° ) − sin ( 45 ° ) sin ( 45 ° ) cos ( 45 ° ) ] = [ 2 2 − 2 2 2 2 2 2 ] \mathbf{A} = \begin{bmatrix} \cos(45°) & -\sin(45°) \\ \sin(45°) & \cos(45°) \end{bmatrix} = \begin{bmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{bmatrix} A = [ cos ( 4 5 ° ) sin ( 4 5 ° ) − sin ( 4 5 ° ) cos ( 4 5 ° ) ] = [ 2 2 2 2 − 2 2 2 2 ]
现在,让我们对向量 v ⃗ = [ 1 0 ] \vec{\mathbf{v}} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} v = [ 1 0 ]
A v ⃗ = [ 2 2 − 2 2 2 2 2 2 ] [ 1 0 ] = [ 2 2 2 2 ] \mathbf{A}\vec{\mathbf{v}} = \begin{bmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} \end{bmatrix} A v = [ 2 2 2 2 − 2 2 2 2 ] [ 1 0 ] = [ 2 2 2 2 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 import numpy as npimport matplotlib.pyplot as pltplt.rcParams['font.sans-serif' ] = ['SimHei' ] plt.rcParams['axes.unicode_minus' ] = False theta = np.pi/4 A = np.array([[np.cos(theta), -np.sin(theta)], [np.sin(theta), np.cos(theta)]]) v = np.array([[1 ], [0 ]]) result = np.dot(A, v) plt.figure(figsize=(12 , 5 )) plt.subplot(121 ) plt.quiver(0 , 0 , v[0 ], v[1 ], angles='xy' , scale_units='xy' , scale=1 , color='b' , label='原始向量' ) plt.grid(True ) plt.axis('equal' ) plt.xlim(-4 , 4 ) plt.ylim(-4 , 4 ) plt.title('原始向量' ) plt.legend() plt.subplot(122 ) plt.quiver(0 , 0 , result[0 ], result[1 ], angles='xy' , scale_units='xy' , scale=1 , color='r' , label='变换后的向量' ) plt.grid(True ) plt.axis('equal' ) plt.xlim(-4 , 4 ) plt.ylim(-4 , 4 ) plt.title('旋转后的向量' ) plt.legend() plt.show() print ("原始向量:" )print (v)print ("\n变换后的向量:" )print (result)
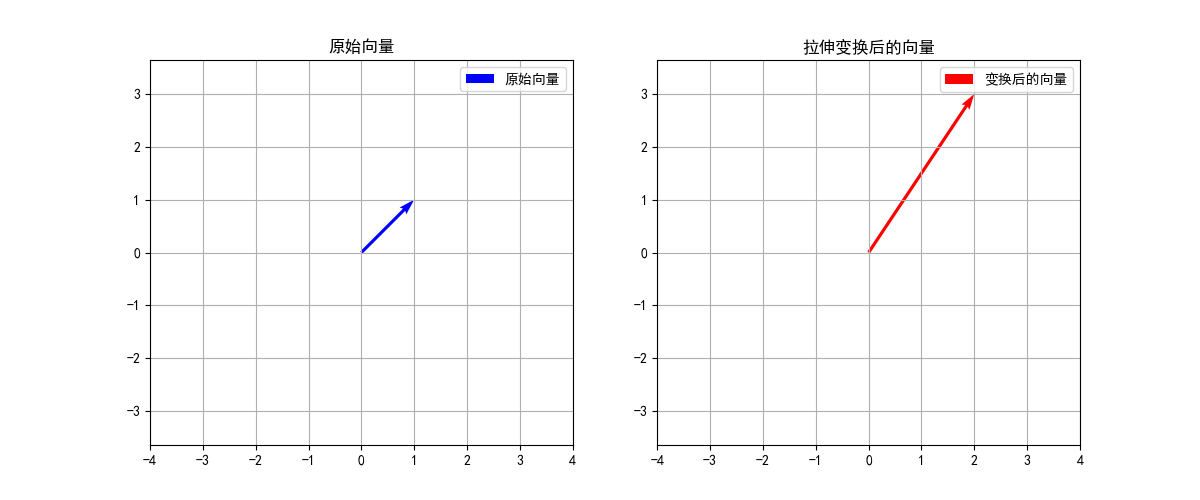
例子:矩阵拉伸变换
拉伸变换矩阵为:
A = [ 2 0 0 3 ] \mathbf{A} = \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix} A = [ 2 0 0 3 ]
让我们对向量 v ⃗ = [ 1 1 ] \vec{\mathbf{v}} = \begin{bmatrix} 1 \\ 1 \end{bmatrix} v = [ 1 1 ]
A v ⃗ = [ 2 0 0 3 ] [ 1 1 ] = [ 2 ⋅ 1 + 0 ⋅ 1 0 ⋅ 1 + 3 ⋅ 1 ] = [ 2 3 ] \mathbf{A}\vec{\mathbf{v}} = \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 \cdot 1 + 0 \cdot 1 \\ 0 \cdot 1 + 3 \cdot 1 \end{bmatrix} = \begin{bmatrix} 2 \\ 3 \end{bmatrix} A v = [ 2 0 0 3 ] [ 1 1 ] = [ 2 ⋅ 1 + 0 ⋅ 1 0 ⋅ 1 + 3 ⋅ 1 ] = [ 2 3 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 import numpy as npimport matplotlib.pyplot as pltplt.rcParams['font.sans-serif' ] = ['SimHei' ] plt.rcParams['axes.unicode_minus' ] = False A = np.array([[2 , 0 ], [0 , 3 ]]) v = np.array([[1 ], [1 ]]) result = np.dot(A, v) plt.figure(figsize=(12 , 5 )) plt.subplot(121 ) plt.quiver(0 , 0 , v[0 ], v[1 ], angles='xy' , scale_units='xy' , scale=1 , color='b' , label='原始向量' ) plt.grid(True ) plt.axis('equal' ) plt.xlim(-4 , 4 ) plt.ylim(-4 , 4 ) plt.title('原始向量' ) plt.legend() plt.subplot(122 ) plt.quiver(0 , 0 , result[0 ], result[1 ], angles='xy' , scale_units='xy' , scale=1 , color='r' , label='变换后的向量' ) plt.grid(True ) plt.axis('equal' ) plt.xlim(-4 , 4 ) plt.ylim(-4 , 4 ) plt.title('拉伸变换后的向量' ) plt.legend() plt.show() print ("原始向量:" )print (v)print ("\n变换后的向量:" )print (result)original_length = np.sqrt(v[0 ]**2 + v[1 ]**2 ) new_length = np.sqrt(result[0 ]**2 + result[1 ]**2 ) print (f"\n原始向量长度: {original_length[0 ]:.2 f} " )print (f"变换后向量长度: {new_length[0 ]:.2 f} " )
矩阵 A \mathbf{A} A 方向保持不变(或反向),只是大小发生了缩放 。这些特殊的向量就叫做矩阵 A \mathbf{A} A 特征向量 ,而缩放的倍数就叫做特征值 。
用数学公式表示就是:
A v ⃗ = λ v ⃗ \mathbf{A}\vec{\mathbf{v}}= λ \vec{\mathbf{v}}
A v = λ v
特征分解 (Eigendecomposition)的公式推导和理解 根据
A v ⃗ = λ v ⃗ \mathbf{A}\vec{\mathbf{v}}= λ \vec{\mathbf{v}}
A v = λ v
如果一个 n × n n×n n × n A \mathbf{A} A n n n { v 1 , v 2 , . . . , v n } \{\mathbf{v}_{1}, \mathbf{v}_{2}, ..., \mathbf{v}_{n}\} { v 1 , v 2 , . . . , v n } { λ 1 , λ 2 , . . . , λ n } \{λ_1, λ_2, ..., λ_n\} { λ 1 , λ 2 , . . . , λ n } P \mathbf{P} P
P = [ v 1 v 2 . . . v n ] \mathbf{P} = [\mathbf{v}_1 \ \mathbf{v}_2 \ ... \ \mathbf{v}_n]
P = [ v 1 v 2 . . . v n ]
将这些特征值组成一个对角矩阵 Λ \mathbf{Λ} Λ
Λ = diag ( λ 1 , λ 2 , . . . , λ n ) = [ λ 1 0 . . . 0 0 λ 2 . . . 0 . . . . . . . . . . . . 0 0 . . . λ n ] \mathbf{Λ} = \text{diag}(λ_1, λ_2, ..., λ_n) = \begin{bmatrix}
λ_1 & 0 & ... & 0 \\
0 & λ_2 & ... & 0 \\
... & ... & ... & ... \\
0 & 0 & ... & λ_n
\end{bmatrix}
Λ = diag ( λ 1 , λ 2 , . . . , λ n ) = ⎣ ⎢ ⎢ ⎢ ⎡ λ 1 0 . . . 0 0 λ 2 . . . 0 . . . . . . . . . . . . 0 0 . . . λ n ⎦ ⎥ ⎥ ⎥ ⎤
根据特征向量和特征值的定义,我们有:
A v 1 = λ 1 v 1 A v 2 = λ 2 v 2 . . . A v n = λ n v n \mathbf{A} \mathbf{v}_1 = λ_1 \mathbf{v}_1 \\
\mathbf{A} \mathbf{v}_2 = λ_2 \mathbf{v}_2 \\
... \\
\mathbf{A} \mathbf{v}_n = λ_n \mathbf{v}_n
A v 1 = λ 1 v 1 A v 2 = λ 2 v 2 . . . A v n = λ n v n
将这些等式组合起来,我们可以得到:
A [ v 1 v 2 . . . v n ] = [ λ 1 v 1 λ 2 v 2 . . . λ n v n ] \mathbf{A} [\mathbf{v}_1 \ \mathbf{v}_2 \ ... \ \mathbf{v}_n] = [λ_1\mathbf{v}_1 \ λ_2\mathbf{v}_2 \ ... \ λ_n\mathbf{v}_n]
A [ v 1 v 2 . . . v n ] = [ λ 1 v 1 λ 2 v 2 . . . λ n v n ]
可以进一步写成:
A P = [ v 1 v 2 . . . v n ] [ λ 1 0 . . . 0 0 λ 2 . . . 0 . . . . . . . . . . . . 0 0 . . . λ n ] \mathbf{A} \mathbf{P} = [\mathbf{v}_1 \ \mathbf{v}_2 \ ... \ \mathbf{v}_n] \begin{bmatrix}
λ_1 & 0 & ... & 0 \\
0 & λ_2 & ... & 0 \\
... & ... & ... & ... \\
0 & 0 & ... & λ_n
\end{bmatrix}
A P = [ v 1 v 2 . . . v n ] ⎣ ⎢ ⎢ ⎢ ⎡ λ 1 0 . . . 0 0 λ 2 . . . 0 . . . . . . . . . . . . 0 0 . . . λ n ⎦ ⎥ ⎥ ⎥ ⎤
即:
A P = P Λ \mathbf{A} \mathbf{P} = \mathbf{P} \mathbf{Λ}
A P = P Λ
由于我们假设特征向量是线性无关的,所以矩阵 P \mathbf{P} P P \mathbf{P} P P − 1 \mathbf{P}^{-1} P − 1
A P P − 1 = P Λ P − 1 \mathbf{A} \mathbf{P} \mathbf{P}^{-1} = \mathbf{P} \mathbf{Λ} \mathbf{P}^{-1}
A P P − 1 = P Λ P − 1
最终得到特征分解的形式:
A = P Λ P − 1 \mathbf{A}= \mathbf{P}\mathbf{Λ}\mathbf{P}^{-1}
A = P Λ P − 1
对实对称矩阵的特征分解公式
任意的 N ×N 实对称矩阵的特征值都是实数且都有 N 个线性无关的特征向量。并且这些特征向量都可以正交单位化而得到一组正交且模为 1 的向量。故实对称矩阵 A 可被分解成
A = P Λ P − 1 = P Λ P T \mathbf{A} =\mathbf{P} \mathbf{\Lambda } \mathbf{P} ^{-1}=\mathbf{P} \mathbf{\Lambda } \mathbf{P} ^{T}
A = P Λ P − 1 = P Λ P T
其中 P 为 正交矩阵, Λ 为实对角矩阵。
一个矩阵 P \mathbf{P} P P \mathbf{P} P
P T P = I \mathbf{P}^T \mathbf{P} = \mathbf{I} P T P = I I \mathbf{I} I
这意味着 P T = P − 1 \mathbf{P}^T = \mathbf{P}^{-1} P T = P − 1 P \mathbf{P} P
只有方阵才能进行特征分解。
(A只能为n×n)
A ⏟ n × n v ⃗ ⏟ n × 1 = λ v ⃗ ⏟ n × 1 \underbrace{\mathbf{A}}_{n \times n}\underbrace{\vec{\mathbf{v}}}_{n \times 1}=
\lambda \underbrace{\vec{\mathbf{v}}}_{n \times 1}
n × n A n × 1 v = λ n × 1 v
并非所有方阵都能进行特征分解。 只有当方阵有 n n n
公式: A = P Λ P − 1 \mathbf{A} = \mathbf{P}\mathbf{Λ}\mathbf{P}^{-1} A = P Λ P − 1
P \mathbf{P} P Λ \mathbf{Λ} Λ P − 1 \mathbf{P}^{-1} P − 1 P \mathbf{P} P
A v ⃗ = ( P Λ P − 1 ) v ⃗ = P ( Λ ( P − 1 v ⃗ ) ) \mathbf{A}\vec{\mathbf{v}}=\left(\mathbf{P\Lambda P}^{-1}\right)\vec{\mathbf{v}} = \mathbf{P}(\mathbf{Λ}(\mathbf{P}^{-1}\vec{\mathbf{v}})) A v = ( P Λ P − 1 ) v = P ( Λ ( P − 1 v ) )
简单理解A v ⃗ \mathbf{A}\vec{\mathbf{v}} A v
将向量 [ 2 1 ] \begin{bmatrix} 2 \\ 1 \end{bmatrix} [ 2 1 ] 特征向量的线性组合 :1 [ 1 0 ] + 1 [ 1 1 ] 1 \begin{bmatrix} 1 \\ 0 \end{bmatrix} + 1 \begin{bmatrix} 1 \\ 1 \end{bmatrix} 1 [ 1 0 ] + 1 [ 1 1 ]
将矩阵 A 作用于该线性组合:A ( 1 [ 1 0 ] + 1 [ 1 1 ] ) = 1 A [ 1 0 ] + 1 A [ 1 1 ] A(1 \begin{bmatrix} 1 \\ 0 \end{bmatrix} + 1 \begin{bmatrix} 1 \\ 1 \end{bmatrix}) = 1A\begin{bmatrix} 1 \\ 0 \end{bmatrix} + 1A\begin{bmatrix} 1 \\ 1 \end{bmatrix} A ( 1 [ 1 0 ] + 1 [ 1 1 ] ) = 1 A [ 1 0 ] + 1 A [ 1 1 ]
利用特征值和特征向量的关系 :1 ( 2 [ 1 0 ] ) + 1 ( 3 [ 1 1 ] ) = 2 [ 1 0 ] + 3 [ 1 1 ] 1(2\begin{bmatrix} 1 \\ 0 \end{bmatrix}) + 1(3\begin{bmatrix} 1 \\ 1 \end{bmatrix}) = 2 \begin{bmatrix} 1 \\ 0 \end{bmatrix} + 3 \begin{bmatrix} 1 \\ 1 \end{bmatrix} 1 ( 2 [ 1 0 ] ) + 1 ( 3 [ 1 1 ] ) = 2 [ 1 0 ] + 3 [ 1 1 ]
计算结果:2 [ 1 0 ] + 3 [ 1 1 ] = [ 5 3 ] 2 \begin{bmatrix} 1 \\ 0 \end{bmatrix} + 3 \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 5 \\ 3 \end{bmatrix} 2 [ 1 0 ] + 3 [ 1 1 ] = [ 5 3 ]
具体变换过程:
P − 1 v ⃗ \mathbf{P}^{-1}\vec{\mathbf{v}} P − 1 v v ⃗ \vec{\mathbf{v}} v
假设 v ⃗ \vec{\mathbf{v}} v x ⃗ \vec{\mathbf{x}} x
根据基变换的原理,我们有:
v ⃗ = P x ⃗ = v ⃗ 1 x 1 + v ⃗ 2 x 2 + . . . + v ⃗ n x n \vec{\mathbf{v}} = \mathbf{P}\vec{\mathbf{x}} = \vec{\mathbf{v}}_1 x_1 + \vec{\mathbf{v}}_2 x_2 + ... + \vec{\mathbf{v}}_n x_n v = P x = v 1 x 1 + v 2 x 2 + . . . + v n x n
其中 x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x 1 , x 2 , . . . , x n x ⃗ \vec{\mathbf{x}} x
为了得到 x ⃗ \vec{\mathbf{x}} x P − 1 \mathbf{P}^{-1} P − 1
P − 1 v ⃗ = P − 1 P x ⃗ = I x ⃗ = x ⃗ \mathbf{P}^{-1}\vec{\mathbf{v}} = \mathbf{P}^{-1}\mathbf{P}\vec{\mathbf{x}} = \mathbf{I}\vec{\mathbf{x}} = \vec{\mathbf{x}} P − 1 v = P − 1 P x = I x = x
因此,P − 1 v ⃗ \mathbf{P}^{-1}\vec{\mathbf{v}} P − 1 v x ⃗ \vec{\mathbf{x}} x v ⃗ \vec{\mathbf{v}} v
Λ ( P − 1 v ⃗ ) \mathbf{Λ}(\mathbf{P}^{-1}\vec{\mathbf{v}}) Λ ( P − 1 v )
P ( Λ ( P − 1 v ⃗ ) ) \mathbf{P}(\mathbf{Λ}(\mathbf{P}^{-1}\vec{\mathbf{v}})) P ( Λ ( P − 1 v ) )
💡理解:
特征分解揭示了矩阵 A \mathbf{A} A A \mathbf{A} A 特征向量 **指明了缩放的方向 ,特征值 **指明了缩放的比例 。
简化计算 特征分解将复杂的矩阵运算简化为对角矩阵的运算。对角矩阵的幂运算和求逆都非常简单,这在计算 A n \mathbf{A}^n A n A \mathbf{A} A
A n = P Λ n P − 1 \mathbf{A}^{n}= \mathbf{P}\mathbf{Λ}^{n}\mathbf{P}^{-1}
A n = P Λ n P − 1
比如,利用特征分解计算斐波那契数列的通项公式
斐波那契数列是一个经典的数列,定义为 F 0 = 0 F_0 = 0 F 0 = 0 F 1 = 1 F_1 = 1 F 1 = 1 n ≥ 2 n \geq 2 n ≥ 2 F n = F n − 1 + F n − 2 F_n = F_{n-1} + F_{n-2} F n = F n − 1 + F n − 2
首先,我们可以将斐波那契数列的递推关系用矩阵形式表示:
[ F n F n − 1 ] = [ 1 1 1 0 ] [ F n − 1 F n − 2 ] \begin{bmatrix} F_n \\ F_{n-1} \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} F_{n-1} \\ F_{n-2} \end{bmatrix}
[ F n F n − 1 ] = [ 1 1 1 0 ] [ F n − 1 F n − 2 ]
设矩阵 A \mathbf{A} A
A = [ 1 1 1 0 ] \mathbf{A} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}
A = [ 1 1 1 0 ]
那么,我们有:
[ F n F n − 1 ] = A n − 1 [ F 1 F 0 ] \begin{bmatrix} F_n \\ F_{n-1} \end{bmatrix} = \mathbf{A}^{n-1} \begin{bmatrix} F_1 \\ F_0 \end{bmatrix}
[ F n F n − 1 ] = A n − 1 [ F 1 F 0 ]
即:
[ F n F n − 1 ] = A n − 1 [ 1 0 ] \begin{bmatrix} F_n \\ F_{n-1} \end{bmatrix} = \mathbf{A}^{n-1} \begin{bmatrix} 1 \\ 0 \end{bmatrix}
[ F n F n − 1 ] = A n − 1 [ 1 0 ]
为了找到 A n − 1 \mathbf{A}^{n-1} A n − 1 A \mathbf{A} A λ \lambda λ
det ( A − λ I ) = 0 \det(\mathbf{A} - \lambda \mathbf{I}) = 0
det ( A − λ I ) = 0
即:
det [ 1 − λ 1 1 − λ ] = ( 1 − λ ) ( − λ ) − 1 = λ 2 − λ − 1 = 0 \det\begin{bmatrix} 1-\lambda & 1 \\ 1 & -\lambda \end{bmatrix} = (1-\lambda)(-\lambda) - 1 = \lambda^2 - \lambda - 1 = 0
det [ 1 − λ 1 1 − λ ] = ( 1 − λ ) ( − λ ) − 1 = λ 2 − λ − 1 = 0
解这个特征方程,我们得到两个特征值:
λ 1 = 1 + 5 2 , λ 2 = 1 − 5 2 \lambda_{1}= \frac{1 + \sqrt{5}}{2}, \quad \lambda_{2}= \frac{1 - \sqrt{5}}{2}
λ 1 = 2 1 + 5 , λ 2 = 2 1 − 5
接下来,计算对应的特征向量。对于 λ 1 \lambda_1 λ 1
[ 1 − λ 1 1 1 − λ 1 ] [ x y ] = [ 0 0 ] \begin{bmatrix} 1-\lambda_1 & 1 \\ 1 & -\lambda_1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}
[ 1 − λ 1 1 1 − λ 1 ] [ x y ] = [ 0 0 ]
解这个方程组,我们得到特征向量 v 1 = [ λ 1 1 ] \mathbf{v}_1 = \begin{bmatrix} \lambda_1 \\ 1 \end{bmatrix} v 1 = [ λ 1 1 ]
类似地,对于 λ 2 \lambda_2 λ 2 v 2 = [ λ 2 1 ] \mathbf{v}_2 = \begin{bmatrix} \lambda_2 \\ 1 \end{bmatrix} v 2 = [ λ 2 1 ]
构造矩阵 P \mathbf{P} P Λ \mathbf{Λ} Λ
P = [ λ 1 λ 2 1 1 ] , Λ = [ λ 1 0 0 λ 2 ] \mathbf{P} = \begin{bmatrix} \lambda_1 & \lambda_2 \\ 1 & 1 \end{bmatrix}, \quad \mathbf{Λ} = \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix}
P = [ λ 1 1 λ 2 1 ] , Λ = [ λ 1 0 0 λ 2 ]
由于 A = P Λ P − 1 \mathbf{A} = \mathbf{P}\mathbf{Λ}\mathbf{P}^{-1} A = P Λ P − 1
A n − 1 = P Λ n − 1 P − 1 \mathbf{A}^{n-1} = \mathbf{P}\mathbf{Λ}^{n-1}\mathbf{P}^{-1}
A n − 1 = P Λ n − 1 P − 1
计算 Λ n − 1 \mathbf{Λ}^{n-1} Λ n − 1
Λ n − 1 = [ λ 1 n − 1 0 0 λ 2 n − 1 ] \mathbf{Λ}^{n-1} = \begin{bmatrix} \lambda_1^{n-1} & 0 \\ 0 & \lambda_2^{n-1} \end{bmatrix}
Λ n − 1 = [ λ 1 n − 1 0 0 λ 2 n − 1 ]
然后,计算 P − 1 \mathbf{P}^{-1} P − 1
P − 1 = 1 λ 1 − λ 2 [ 1 − λ 2 − 1 λ 1 ] \mathbf{P}^{-1} = \frac{1}{\lambda_1 - \lambda_2} \begin{bmatrix} 1 & -\lambda_2 \\ -1 & \lambda_1 \end{bmatrix}
P − 1 = λ 1 − λ 2 1 [ 1 − 1 − λ 2 λ 1 ]
将这些代入 A n − 1 \mathbf{A}^{n-1} A n − 1 F n F_n F n
F n = [ 1 0 ] A n − 1 [ 1 0 ] F_n = \begin{bmatrix} 1 & 0 \end{bmatrix} \mathbf{A}^{n-1} \begin{bmatrix} 1 \\ 0 \end{bmatrix}
F n = [ 1 0 ] A n − 1 [ 1 0 ]
经过计算,我们得到斐波那契数列的通项公式:
F n = 1 5 ( ( 1 + 5 2 ) n − ( 1 − 5 2 ) n ) F_n = \frac{1}{\sqrt{5}} \left( \left(\frac{1 + \sqrt{5}}{2}\right)^n - \left(\frac{1 - \sqrt{5}}{2}\right)^n \right)
F n = 5 1 ( ( 2 1 + 5 ) n − ( 2 1 − 5 ) n )
这个公式称为斐波那契数列的Binet公式 ,它提供了一种直接计算斐波那契数列中任意项的方法,而无需递归计算。这个公式也说明了为什么斐波那契数列中连续两个数的比值会随着数列的增长会越来越接近黄金分割。
PCA是一种用于降维的技术,目的在于通过找到数据中方差最大的方向来减少数据的维度,同时尽可能保留数据的主要信息。
PCA的核心,是要寻找一组基组成的矩阵左乘原矩阵,使得 **n **维特征映射到k
主成分分析(PCA),可以通过特征值分解 或奇异值分解 来实现。PCA通过对协方差矩阵的特征分解,找到了数据的主成分方向,实现了有效的降维。特征分解是PCA实现的核心步骤。
PCA计算步骤:
去中心化原始维度数据(只需要减均值即可,不必标准化方差);
协方差矩阵 :
计算数据特征的协方差矩阵 C \mathbf{C} C
特征分解 :
对协方差矩阵 C \mathbf{C} C
C = P Λ P − 1 \mathbf{C} = \mathbf{P}\mathbf{\Lambda}\mathbf{P}^{-1}
C = P Λ P − 1
其中,P \mathbf{P} P Λ \mathbf{\Lambda} Λ
由于协方差矩阵是对称矩阵,所以可以写成
C = P Λ P − 1 = P Λ P T \mathbf{C} =\mathbf{P} \mathbf{\Lambda } \mathbf{P} ^{-1}=\mathbf{P} \mathbf{\Lambda } \mathbf{P} ^{T}
C = P Λ P − 1 = P Λ P T
选择主成分 :
特征值表示了对应特征向量方向上的方差大小。选择特征值最大的几个特征向量作为主成分。
这些主成分对应的数据方向保留了最多的信息。
降维 :
💡总结
特征值 :在PCA中,特征值表示了数据在对应特征向量方向上的方差大小 。特征向量 :代表了数据的主成分方向,即特征空间的基向量 。降维过程 :通过选择最大特征值对应的特征向量 ,将数据投影到一个较低维度的空间中。
备注
PCA通常使用奇异值分解(SVD)而不是直接使用特征分解。这是因为SVD在数值稳定性和计算效率上具有优势。以下是一些具体原因:
SVD的优势
数值稳定性 :
计算效率 :
对于高维数据,直接计算协方差矩阵并进行特征分解可能会非常耗时。SVD可以直接在原始数据矩阵上操作,避免构造协方差矩阵。
PCA通过SVD实现的步骤
数据中心化 :
将数据矩阵 X \mathbf{X} X
SVD分解 :
选择主成分 :
Σ \mathbf{\Sigma} Σ
降维 :
使用 V \mathbf{V} V
特征值和特征向量计算步骤:
构造特征方程:
将定义式 A v = λ v A\mathbf{v}= \lambda\mathbf{v} A v = λ v
A v − λ v = 0 A\mathbf{v} - \lambda\mathbf{v} = \mathbf{0}
A v − λ v = 0
将 λ 乘以单位矩阵 I(与 A 同阶),得到:
A v − λ I v = 0 A\mathbf{v} - \lambda I\mathbf{v} = \mathbf{0}
A v − λ I v = 0
提取公因式 v :
( A − λ I ) v = 0 (A - \lambda I)\mathbf{v} = \mathbf{0}
( A − λ I ) v = 0
要使上式存在非零解 v ,矩阵 ( A − λ I ) (A - \lambda I) ( A − λ I ) 特征方程 :
d e t ( A − λ I ) = 0 det(A - \lambda I) = 0
d e t ( A − λ I ) = 0
求解特征值:
计算行列式 d e t ( A − λ I ) det(A - \lambda I) d e t ( A − λ I ) 特征多项式 。
求解特征向量:
对于每一个求得的特征值 λ,将其代入方程 ( A − λ I ) v = 0 (A - \lambda I)\mathbf{v} = \mathbf{0} ( A − λ I ) v = 0
💡总结一下:
特征值 λ: 通过解特征方程 d e t ( A − λ I ) = 0 det(A - \lambda I) = 0 d e t ( A − λ I ) = 0 特征向量 v: 对于每个特征值 λ,通过解齐次线性方程组 ( A − λ I ) v = 0 (A - \lambda I)\mathbf{v} = \mathbf{0} ( A − λ I ) v = 0
特征值和特征向量计算的 求解例子现在我们用你提供的矩阵 A 来计算特征值和特征向量:
A = [ 4 6 0 − 3 − 5 0 − 3 − 6 1 ] A = \begin{bmatrix} 4 & 6 & 0 \\ -3 & -5 & 0 \\ -3 & -6 & 1 \end{bmatrix}
A = ⎣ ⎢ ⎡ 4 − 3 − 3 6 − 5 − 6 0 0 1 ⎦ ⎥ ⎤
1. 构造特征方程, 求解特征值 A − λ I = [ 4 6 0 − 3 − 5 0 − 3 − 6 1 ] − λ [ 1 0 0 0 1 0 0 0 1 ] = [ 4 − λ 6 0 − 3 − 5 − λ 0 − 3 − 6 1 − λ ] A - \lambda I = \begin{bmatrix} 4 & 6 & 0 \\ -3 & -5 & 0 \\ -3 & -6 & 1 \end{bmatrix} - \lambda \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 4-\lambda & 6 & 0 \\ -3 & -5-\lambda & 0 \\ -3 & -6 & 1-\lambda \end{bmatrix}
A − λ I = ⎣ ⎢ ⎡ 4 − 3 − 3 6 − 5 − 6 0 0 1 ⎦ ⎥ ⎤ − λ ⎣ ⎢ ⎡ 1 0 0 0 1 0 0 0 1 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 4 − λ − 3 − 3 6 − 5 − λ − 6 0 0 1 − λ ⎦ ⎥ ⎤
计算行列式:
d e t ( A − λ I ) = ∣ 4 − λ 6 0 − 3 − 5 − λ 0 − 3 − 6 1 − λ ∣ det(A - \lambda I) =
\begin{vmatrix}
4-\lambda & 6 & 0 \\
-3 & -5-\lambda & 0 \\
-3 & -6 & 1-\lambda
\end{vmatrix}
d e t ( A − λ I ) = ∣ ∣ ∣ ∣ ∣ ∣ ∣ 4 − λ − 3 − 3 6 − 5 − λ − 6 0 0 1 − λ ∣ ∣ ∣ ∣ ∣ ∣ ∣
由于第三列只有一个非零元素,我们可以按第三列展开:
d e t ( A − λ I ) = ( 1 − λ ) ∣ 4 − λ 6 − 3 − 5 − λ ∣ det(A - \lambda I) = (1-\lambda) \begin{vmatrix} 4-\lambda & 6 \\ -3 & -5-\lambda \end{vmatrix}
d e t ( A − λ I ) = ( 1 − λ ) ∣ ∣ ∣ ∣ ∣ 4 − λ − 3 6 − 5 − λ ∣ ∣ ∣ ∣ ∣
这里利用了行列式的性质(代数余子式),具体见线性代数丨行列式
计算 2x2 行列式:
∣ 4 − λ 6 − 3 − 5 − λ ∣ = ( 4 − λ ) ( − 5 − λ ) − ( 6 ) ( − 3 ) = − 20 − 4 λ + 5 λ + λ 2 + 18 = λ 2 + λ − 2 \begin{vmatrix} 4-\lambda & 6 \\ -3 & -5-\lambda \end{vmatrix} = (4-\lambda)(-5-\lambda) - (6)(-3) = -20 - 4\lambda + 5\lambda + \lambda^2 + 18 = \lambda^2 + \lambda - 2
∣ ∣ ∣ ∣ ∣ 4 − λ − 3 6 − 5 − λ ∣ ∣ ∣ ∣ ∣ = ( 4 − λ ) ( − 5 − λ ) − ( 6 ) ( − 3 ) = − 2 0 − 4 λ + 5 λ + λ 2 + 1 8 = λ 2 + λ − 2
所以,特征方程为:
( 1 − λ ) ( λ 2 + λ − 2 ) = 0 (1-\lambda)(\lambda^{2}+ \lambda - 2) = 0
( 1 − λ ) ( λ 2 + λ − 2 ) = 0
解特征方程:
( 1 − λ ) ( λ + 2 ) ( λ − 1 ) = 0 (1-\lambda)(\lambda+2)(\lambda-1) = 0
( 1 − λ ) ( λ + 2 ) ( λ − 1 ) = 0
得到特征值:
λ 1 = 1 , λ 2 = − 2 , λ 3 = 1 \lambda_1 = 1, \quad \lambda_2 = -2, \quad \lambda_3 = 1
λ 1 = 1 , λ 2 = − 2 , λ 3 = 1
注意,特征值可以重复。在这个例子中,λ = 1 是一个二重特征值。
. 求解特征向量
对于特征值 λ₁ = 1:
将 λ = 1 代入 ( A − λ I ) v = 0 (A - \lambda I)\mathbf{v}= \mathbf{0} ( A − λ I ) v = 0
[ 4 − 1 6 0 − 3 − 5 − 1 0 − 3 − 6 1 − 1 ] [ x y z ] = [ 3 6 0 − 3 − 6 0 − 3 − 6 0 ] [ x y z ] = [ 0 0 0 ] \begin{bmatrix}
4-1 & 6 & 0 \\
-3 & -5-1 & 0 \\
-3 & -6 & 1-1
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z
\end{bmatrix}
=
\begin{bmatrix}
3 & 6 & 0 \\
-3 & -6 & 0 \\
-3 & -6 & 0
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0
\end{bmatrix}
⎣ ⎢ ⎡ 4 − 1 − 3 − 3 6 − 5 − 1 − 6 0 0 1 − 1 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ x y z ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 3 − 3 − 3 6 − 6 − 6 0 0 0 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ x y z ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 0 0 0 ⎦ ⎥ ⎤
得到线性方程组:
{ 3 x + 6 y = 0 − 3 x − 6 y = 0 − 3 x − 6 y = 0 \begin{cases}
3x + 6y = 0 \\
-3x - 6y = 0 \\
-3x - 6y = 0
\end{cases}
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 3 x + 6 y = 0 − 3 x − 6 y = 0 − 3 x − 6 y = 0
这三个方程是等价的,化简得到:
x + 2 y = 0 x + 2y = 0
x + 2 y = 0
令 y = t,则 x = -2t。z 是自由变量,可以取任意值,令 z = s。
所以,对应于特征值 λ₁ = 1 的特征向量为:
v 1 = [ − 2 t t s ] = t [ − 2 1 0 ] + s [ 0 0 1 ] \mathbf{v}_{1}=
\begin{bmatrix}
-2t \\
t \\
s
\end{bmatrix}
= t
\begin{bmatrix}
-2 \\
1 \\
0
\end{bmatrix}
+ s
\begin{bmatrix}
0 \\
0 \\
1
\end{bmatrix}
v 1 = ⎣ ⎢ ⎡ − 2 t t s ⎦ ⎥ ⎤ = t ⎣ ⎢ ⎡ − 2 1 0 ⎦ ⎥ ⎤ + s ⎣ ⎢ ⎡ 0 0 1 ⎦ ⎥ ⎤
由于 λ = 1 是二重特征值,我们得到了两个线性无关的特征向量。通常我们取一组基,例如当 t=1, s=0 和 t=0, s=1 时:
v 1 a = [ − 2 1 0 ] , v 1 b = [ 0 0 1 ] \mathbf{v}_{1a}=
\begin{bmatrix}
-2 \\
1 \\
0
\end{bmatrix}, \quad \mathbf{v}_{1b}=
\begin{bmatrix}
0 \\
0 \\
1
\end{bmatrix}
v 1 a = ⎣ ⎢ ⎡ − 2 1 0 ⎦ ⎥ ⎤ , v 1 b = ⎣ ⎢ ⎡ 0 0 1 ⎦ ⎥ ⎤
对于特征值 λ₂ = -2:
将 λ = -2 代入 $$(A - \lambda I)\mathbf{v} = \mathbf{0}$$:
[ 4 − ( − 2 ) 6 0 − 3 − 5 − ( − 2 ) 0 − 3 − 6 1 − ( − 2 ) ] [ x y z ] = [ 6 6 0 − 3 − 3 0 − 3 − 6 3 ] [ x y z ] = [ 0 0 0 ] \begin{bmatrix}4-(-2)&6&0 \\ -3&-5-(-2)&0 \\ -3&-6&1-(-2) \end{bmatrix}
\begin{bmatrix}
x \\
y \\
z
\end{bmatrix}
=
\begin{bmatrix}
6 & 6 & 0 \\
-3 & -3 & 0 \\
-3 & -6 & 3
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0
\end{bmatrix}
⎣ ⎢ ⎡ 4 − ( − 2 ) − 3 − 3 6 − 5 − ( − 2 ) − 6 0 0 1 − ( − 2 ) ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ x y z ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 6 − 3 − 3 6 − 3 − 6 0 0 3 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ x y z ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 0 0 0 ⎦ ⎥ ⎤
得到线性方程组:
{ 6 x + 6 y = 0 − 3 x − 3 y = 0 − 3 x − 6 y + 3 z = 0 \begin{cases}6x + 6y = 0 \\ -3x - 3y = 0 \\ -3x - 6y + 3z = 0 \end{cases}
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 6 x + 6 y = 0 − 3 x − 3 y = 0 − 3 x − 6 y + 3 z = 0
前两个方程等价,化简得到 x + y = 0,即 y = -x。将 y = -x 代入第三个方程:
3 x − 6 ( − x ) + 3 z = 0 3x - 6(-x) + 3z = 0
3 x − 6 ( − x ) + 3 z = 0
3 x + 6 x + 3 z = 0 3x + 6x + 3z = 0
3 x + 6 x + 3 z = 0
x + 3 z = 0 x + 3z = 0
x + 3 z = 0
令 x = k,则 y = -k,z = -k。
所以,对应于特征值 λ₂ = -2 的特征向量为:
v 2 = [ k − k − k ] = k [ 1 − 1 − 1 ] \mathbf{v}_{2} =
\begin{bmatrix}
k \\
-k \\
-k
\end{bmatrix}
= k
\begin{bmatrix}
1 \\
-1 \\
-1
\end{bmatrix}
v 2 = ⎣ ⎢ ⎡ k − k − k ⎦ ⎥ ⎤ = k ⎣ ⎢ ⎡ 1 − 1 − 1 ⎦ ⎥ ⎤
通常我们取 k = 1,得到一个特征向量:
v 2 = [ 1 − 1 − 1 ] \mathbf{v}_{2}=
\begin{bmatrix}
1 \\
-1 \\
-1
\end{bmatrix}
v 2 = ⎣ ⎢ ⎡ 1 − 1 − 1 ⎦ ⎥ ⎤
对于成对比较矩阵来说,特征向量就代表着各个因素的权重
对于一致性的成对比较矩阵而言,第一列其实就是特征向量的比例
在实际应用中,由于人为设置的判断矩阵往往存在不一致性,因此需要计算特征向量来近似表示权重向量。而使用传统的特征值计算方式,计算量太大,所以层次分析法算特征向量可以使用简单的几何平均法和算术平均法算特征向量。几何平均法和算术平均法算特征向量的思想就是,用平均化来消除成对比较中的差异,算出一个平均权重。
假设你正在计划一次旅行,有几个目的地可供选择。为了做出最佳决策,你需要考虑多个因素,比如旅游成本、景点吸引力、住宿条件、餐饮质量 等。每个因素的重要性可以用权重来表示,假设这些权重分别为:w 1 , w 2 , w 3 , w 4 w_1, w_2, w_3, w_4 w 1 , w 2 , w 3 , w 4
我们可能不知道每个因素的绝对重要性,但可以通过成对比较来了解它们之间的相对重要性。例如,如果你想比较“景点吸引力”和“旅游成本”,你可能会觉得景点吸引力比旅游成本重要5倍。我们用 a 21 a_{21} a 2 1
所有因素两两比较,得到一个判断矩阵:
旅游成本 景点吸引力 住宿条件 餐饮质量 旅游成本 a 11 a 12 a 13 a 14 景点吸引力 a 21 a 22 a 23 a 24 住宿条件 a 31 a 32 a 33 a 34 餐饮质量 a 41 a 42 a 43 a 44 \begin{array}{c|cccc}
& \text{旅游成本} & \text{景点吸引力} & \text{住宿条件} & \text{餐饮质量} \\
\hline
\text{旅游成本} & a_{11} & a_{12} & a_{13} & a_{14} \\
\text{景点吸引力} & a_{21} & a_{22} & a_{23} & a_{24} \\
\text{住宿条件} & a_{31} & a_{32} & a_{33} & a_{34} \\
\text{餐饮质量} & a_{41} & a_{42} & a_{43} & a_{44} \\
\end{array}
旅游成本 景点吸引力 住宿条件 餐饮质量 旅游成本 a 1 1 a 2 1 a 3 1 a 4 1 景点吸引力 a 1 2 a 2 2 a 3 2 a 4 2 住宿条件 a 1 3 a 2 3 a 3 3 a 4 3 餐饮质量 a 1 4 a 2 4 a 3 4 a 4 4
在这个背景下,我们假设 y 2 y_2 y 2
y 2 = a 21 ∗ w 1 + a 22 ∗ w 2 + a 23 ∗ w 3 + a 24 ∗ w 4 ( 1 ) y_2 = a_{21} * w_1 + a_{22} * w_2 + a_{23} * w_3 + a_{24} * w_4 \quad (1)
y 2 = a 2 1 ∗ w 1 + a 2 2 ∗ w 2 + a 2 3 ∗ w 3 + a 2 4 ∗ w 4 ( 1 )
这里,a 21 a_{21} a 2 1 w 1 w_1 w 1
y 2 = 4 ∗ w 2 ( 2 ) y_{2} = 4 * w_{2} \quad (2)
y 2 = 4 ∗ w 2 ( 2 )
这表示“景点吸引力”的得分是其权重 w 2 w_2 w 2
为了更系统地处理所有因素,我们可以为每个因素(y 1 y_1 y 1 y 4 y_4 y 4
y 1 = a 11 ∗ w 1 + a 12 ∗ w 2 + a 13 ∗ w 3 + a 14 ∗ w 4 y 2 = a 21 ∗ w 1 + a 22 ∗ w 2 + a 23 ∗ w 3 + a 24 ∗ w 4 y 3 = a 31 ∗ w 1 + a 32 ∗ w 2 + a 33 ∗ w 3 + a 34 ∗ w 4 y 4 = a 41 ∗ w 1 + a 42 ∗ w 2 + a 43 ∗ w 3 + a 44 ∗ w 4 \begin{aligned}
y_{1} & = a_{11}* w_{1}+ a_{12}* w_{2}+ a_{13}* w_{3}+ a_{14}* w_{4} \\
y_{2} & = a_{21}* w_{1}+ a_{22}* w_{2}+ a_{23}* w_{3}+ a_{24}* w_{4} \\
y_{3} & = a_{31}* w_{1}+ a_{32}* w_{2}+ a_{33}* w_{3}+ a_{34}* w_{4} \\
y_{4} & = a_{41}* w_{1}+ a_{42}* w_{2}+ a_{43}* w_{3}+ a_{44}* w_{4} \\
\end{aligned}
y 1 y 2 y 3 y 4 = a 1 1 ∗ w 1 + a 1 2 ∗ w 2 + a 1 3 ∗ w 3 + a 1 4 ∗ w 4 = a 2 1 ∗ w 1 + a 2 2 ∗ w 2 + a 2 3 ∗ w 3 + a 2 4 ∗ w 4 = a 3 1 ∗ w 1 + a 3 2 ∗ w 2 + a 3 3 ∗ w 3 + a 3 4 ∗ w 4 = a 4 1 ∗ w 1 + a 4 2 ∗ w 2 + a 4 3 ∗ w 3 + a 4 4 ∗ w 4
即
Y = [ y 1 y 2 y 3 y 4 ] = [ a 11 a 12 a 13 a 14 a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44 ] [ w 1 w 2 w 3 w 4 ] = A w Y = \begin{bmatrix}
y_{1} \\
y_{2} \\
y_{3} \\
y_{4}
\end{bmatrix}
=
\begin{bmatrix}
a_{11} & a_{12} & a_{13} & a_{14} \\
a_{21} & a_{22} & a_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34} \\
a_{41} & a_{42} & a_{43} & a_{44}
\end{bmatrix}
\begin{bmatrix}
w_{1} \\
w_{2} \\
w_{3} \\
w_{4}
\end{bmatrix} = Aw
Y = ⎣ ⎢ ⎢ ⎢ ⎡ y 1 y 2 y 3 y 4 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 a 3 1 a 4 1 a 1 2 a 2 2 a 3 2 a 4 2 a 1 3 a 2 3 a 3 3 a 4 3 a 1 4 a 2 4 a 3 4 a 4 4 ⎦ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ w 1 w 2 w 3 w 4 ⎦ ⎥ ⎥ ⎥ ⎤ = A w
这可以表示为矩阵方程:
Y = A ∗ w Y = A * w
Y = A ∗ w
其中:
Y 是结果贡献的向量,代表每个因素的综合得分。A 是成对比较矩阵,描述了每个因素相对于其他因素的重要性。w 是我们想要确定的权重向量,表示每个因素的相对重要性。
又从等式 (2) 可以看出,Y 的每个元素都等于 w 的相应元素乘以一个常数。我们将此常数表示为 λ λ λ
Y = λ ∗ w Y = λ * w
Y = λ ∗ w
结合矩阵方程,我们得到:
A ∗ w = λ ∗ w A * w = λ * w
A ∗ w = λ ∗ w
而这就是特征向量和特征值的定义!
在层次分析法(AHP)中,通过找到与成对比较矩阵的最大特征值相关联的特征向量,我们就可以获得最能代表所比较因素相对重要性的权重向量。
在理想情况下,如果判断矩阵具有完美的一致性,不同列与第一列只是差一个倍数,只有第一列有信息,那么矩阵的第一列归一化后实际上等于特征向量归一化的结果,且矩阵的最大特征值 λ max \lambda_{\text{max}} λ max n n n
一个判断矩阵 A = [ a i j ] A = [a_{ij}] A = [ a i j ]
对于任意三个因素 i i i j j j k k k i i i j j j a i j a_{ij} a i j j j j k k k a j k a_{jk} a j k i i i k k k a i j × a j k a_{ij} \times a_{jk} a i j × a j k
a i j ⋅ a j k = a i k , ∀ i , j , k a_{ij} \cdot a_{jk} = a_{ik}, \quad \forall i, j, k
a i j ⋅ a j k = a i k , ∀ i , j , k
并且
a i i = 1 , a i j = 1 a j i , ∀ i , j a_{ii} = 1, \quad a_{ij} = \frac{1}{a_{ji}}, \quad \forall i, j
a i i = 1 , a i j = a j i 1 , ∀ i , j
以一个四维一致阵为例:
( 1 a 12 = 1 a 21 a 13 = 1 a 31 a 14 = 1 a 41 a 21 1 a 23 = a 21 ⋅ a 13 a 24 = a 21 ⋅ a 14 a 31 a 32 = a 31 ⋅ a 12 1 a 34 = a 31 ⋅ a 14 a 41 a 42 = a 41 ⋅ a 12 a 43 = a 41 ⋅ a 13 1 ) \begin{pmatrix} 1&a_{12}=\frac{1}{a_{21}}&a_{13}=\frac{1}{a_{31}}&a_{14}=\frac{1}{a_{41}}\\ a_{21}&1& a_{23}= a_{21}\cdot a_{13}&a_{24}= a_{21}\cdot a_{14}\\ a_{31}&a_{32}= a_{31}\cdot a_{12}&1&a_{34}= a_{31}\cdot a_{14}\\ a_{41}&a_{42}= a_{41}\cdot a_{12}&a_{43}= a_{41}\cdot a_{13}&1\\ \end{pmatrix} ⎝ ⎜ ⎜ ⎜ ⎛ 1 a 2 1 a 3 1 a 4 1 a 1 2 = a 2 1 1 1 a 3 2 = a 3 1 ⋅ a 1 2 a 4 2 = a 4 1 ⋅ a 1 2 a 1 3 = a 3 1 1 a 2 3 = a 2 1 ⋅ a 1 3 1 a 4 3 = a 4 1 ⋅ a 1 3 a 1 4 = a 4 1 1 a 2 4 = a 2 1 ⋅ a 1 4 a 3 4 = a 3 1 ⋅ a 1 4 1 ⎠ ⎟ ⎟ ⎟ ⎞
python代码验证
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 import numpy as npa21, a31, a41 = 2 , 3 , 4 A = np.array([ [1 , 1 /a21, 1 /a31, 1 /a41], [a21, 1 , a21/a31, a21/a41], [a31, a31/a21, 1 , a31/a41], [a41, a41/a21, a41/a31, 1 ] ]) eigenvalues, eigenvectors = np.linalg.eig(A) max_index = np.argmax(eigenvalues) max_eigenvalue = eigenvalues[max_index] max_eigenvector = eigenvectors[:, max_index] sum_of_elements = np.sum (max_eigenvector) normalized_max_eigenvector = max_eigenvector / sum_of_elements print ("最大特征值:" , max_eigenvalue) print ("归一化的特征向量:" , normalized_max_eigenvector)
例如,假设我们有一个完美一致的判断矩阵 A A A
A = [ 1 2 4 0.5 1 2 0.25 0.5 1 ] A =
\begin{bmatrix}
1 & 2 & 4 \\
0.5 & 1 & 2 \\
0.25 & 0.5 & 1
\end{bmatrix}
A = ⎣ ⎢ ⎡ 1 0 . 5 0 . 2 5 2 1 0 . 5 4 2 1 ⎦ ⎥ ⎤
在这个理想矩阵中,矩阵的最大特征值 λ max \lambda_{\text{max}} λ max n = 3 n = 3 n = 3
w = [ w 1 w 2 w 3 ] ∝ [ 1 0.5 0.25 ] w =
\begin{bmatrix}
w_{1} \\
w_{2} \\
w_{3}
\end{bmatrix}
\propto
\begin{bmatrix}
1 \\
0.5 \\
0.25
\end{bmatrix}
w = ⎣ ⎢ ⎡ w 1 w 2 w 3 ⎦ ⎥ ⎤ ∝ ⎣ ⎢ ⎡ 1 0 . 5 0 . 2 5 ⎦ ⎥ ⎤
为了得到权重向量,我们只需要对第一列进行归一化处理,即第一列每个元素除以所有元素的总和:
w = 1 1 + 0.5 + 0.25 [ 1 0.5 0.25 ] = [ 0.571 0.286 0.143 ] w = \frac{1}{1 + 0.5 + 0.25}
\begin{bmatrix}
1 \\
0.5 \\
0.25
\end{bmatrix}
=
\begin{bmatrix}
0.571 \\
0.286 \\
0.143
\end{bmatrix}
w = 1 + 0 . 5 + 0 . 2 5 1 ⎣ ⎢ ⎡ 1 0 . 5 0 . 2 5 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 0 . 5 7 1 0 . 2 8 6 0 . 1 4 3 ⎦ ⎥ ⎤
代码验证
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 import numpy as npdef is_consistent (matrix ): """检查矩阵是否为完美一致的判断矩阵""" n = matrix.shape[0 ] for i in range (n): for j in range (n): for k in range (n): if not np.isclose(matrix[i, j] * matrix[j, k], matrix[i, k]): return False return True def normalize_vector (vector ): """归一化向量,使其元素和为1""" return vector / np.sum (vector) def main (): A = np.array([[1 , 2 , 4 ], [0.5 , 1 , 2 ], [0.25 , 0.5 , 1 ]]) if is_consistent(A): print ("矩阵是完美一致的。" ) first_column = A[:, 0 ] normalized_first_column = normalize_vector(first_column) eigvals, eigvecs = np.linalg.eig(A) max_eigval_index = np.argmax(eigvals) principal_eigvec = eigvecs[:, max_eigval_index].real normalized_principal_eigvec = normalize_vector(principal_eigvec) print ("归一化的第一列:" , normalized_first_column) print ("归一化的特征向量:" , normalized_principal_eigvec) if np.allclose(normalized_first_column, normalized_principal_eigvec): print ("第一列是特征向量的比例形式。" ) else : print ("第一列不是特征向量的比例形式。" ) else : print ("矩阵不是完美一致的。" ) if __name__ == "__main__" : main()
根本不需要去用复杂方法算特征向量。
然而,在实际应用中,由于人为设置的判断矩阵往往存在不一致性,因此需要计算特征向量来近似表示权重向量。
而计算判断矩阵 A A A w w w
A ∗ w = λ ∗ w A * w = \lambda * w
A ∗ w = λ ∗ w
用上面方程去算的话,又太过复杂了,需要先通过解特征方程 d e t ( A − λ I ) = 0 det(A - \lambda I) = 0 d e t ( A − λ I ) = 0 ( A − λ I ) v = 0 (A - \lambda I)\mathbf{v} = \mathbf{0} ( A − λ I ) v = 0
而几何平均法和算术平均法算权重向量(特征向量)的思想就是,用平均化来消除差异,算出一个平均权重,得到的平均权重就是近似的特征向量。
由于这个方法,需要矩阵具有一致性,所以需要判断矩阵的一致性比率
考虑到一致性矩阵的最大特征值 λ max \lambda_{\text{max}} λ max n n n
因此矩阵的一致性比率可以用如下公式定义:
CI = λ max − n n − 1 \text{CI}= \frac{\lambda_{\text{max}}- n}{n - 1}
CI = n − 1 λ max − n
而最大特征根的计算公式为:
λ m a x = ( 1 / n ) ∑ i = 1 n ( A w ) i / w i λ_{max} = (1/n)∑_{i=1}^{n} (Aw)_{i}/w_{i}
λ m a x = ( 1 / n ) i = 1 ∑ n ( A w ) i / w i
其实就是把计算的多个特征向量代入 A w = λ ∗ w A w = \lambda * w A w = λ ∗ w λ λ λ