什么是ANOVA方差分析？

ANOVA（Analysis of Variance，方差分析）是一种统计方法，在某些场合也被称为F检验（不过F检验指的实际是方差齐性检验），它用于比较三个或更多样本组之间的均值差异。它通过分析组内和组间的方差，来判断不同组别之间的均值是否存在显著差异。ANOVA的基本思想是，如果不同组的均值存在显著差异，那么这些组之间的方差应当大于组内的方差。

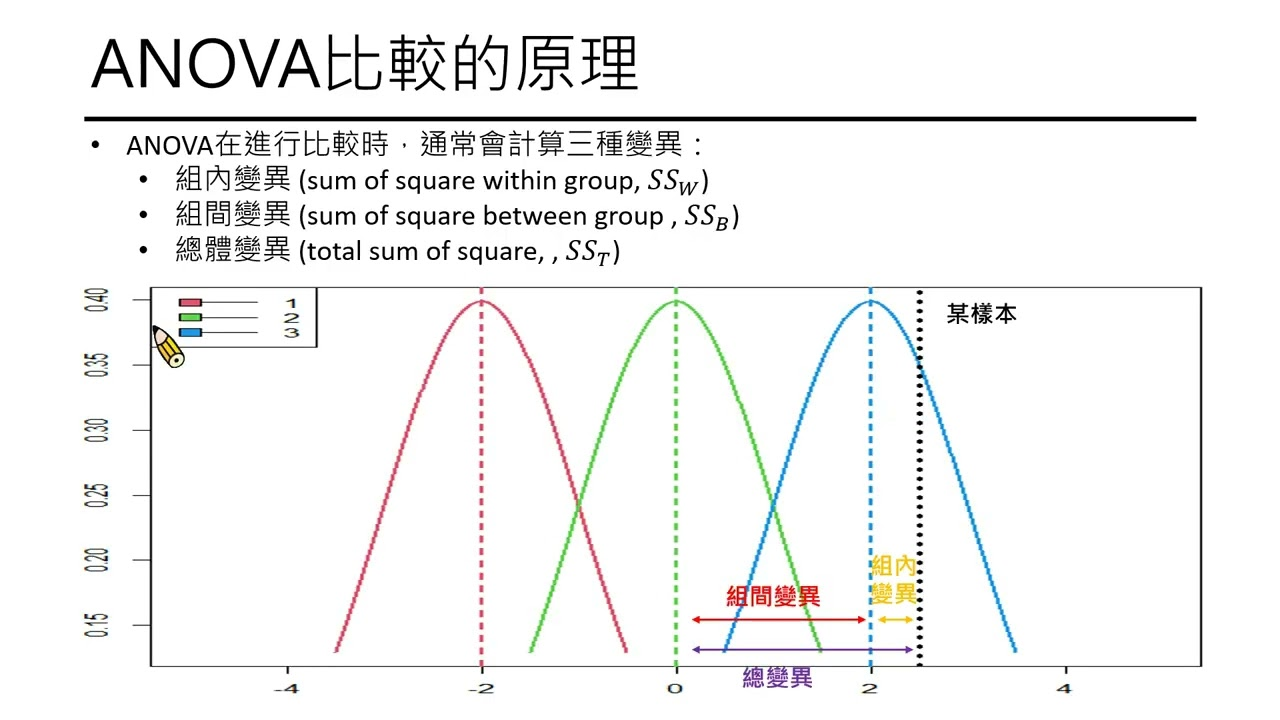
如果不同组的均值存在显著差异，那么这些组之间的方差应当大于组内的方差
如果不同组的均值存在显著差异，那么这些组之间的方差应当大于组内的方差

方差分析依靠F-分布为概率分布的依据，利用平方和（Sum of square）与自由度（Degree of freedom）所计算的组间与组内均方（Mean of square）估计出F值，若有显著差异则考量进行事后比较或称多重比较（Multiple comparison），较常见的为Scheffé's method、Tukey's range test与Bonferroni correction，用于具体探讨其各组之间的差异。。

在方差分析的基本运算概念下，依照所感兴趣的因子数量而可分为单因子方差分析、双因子方差分析、多因子方差分析三大类，依照因子的特性不同而有三种类型，固定效应方差分析（fixed-effect analysis of variance）、随机效应方差分析（random-effect analysis of variance）与混合效应方差分析（Mixed-effect analaysis of variance）

方差分析优于两组比较的T检验之处，在于后者会导致多重比较（multiple comparisons）的问题而致使第一类错误（假阳性导致的假科学论断）的机会增高，因此比较多组平均数是否有差异则是方差分析的主要命题。

ANOVA分析的适用条件

  • 数据独立性：各组样本之间必须是独立的。
  • 正态性：各组样本数据应服从正态分布。
  • 方差齐性：各组样本的方差应该相等。
  • 因变量是连续变量：因变量通常是连续的，且是定量数据。

注意，ANOVA可以用于不均衡样本

ANOVA 方差分析与其他检验方法的关系

T检验

  • t检验：主要用于比较两个独立样本或配对样本的均值差异。常见的有独立样本t检验和配对样本t检验。
  • ANOVA：当需要比较三个或更多组的均值差异，不适合用t检验，适合用ANOVA方差分析。最常见的是单因素方差分析（One-Way ANOVA），它用于比较一个因素的多个水平对因变量的影响。

非参数检验替代方法

ANOVA（Analysis of Variance）是一种常见的分析方法，但要求数据满足正态性、同方差等假设，适用范围受限。

下面是其非参数检验的替代方法

  • Kruskal-Wallis检验：这是单因素ANOVA的非参数替代方法，是非参数版的anova1。它用于比较三个或更多独立组的中位数是否相等。Kruskal-Wallis检验是基于数据的秩而非原始数据值的，实质上是两独立样本时的Mann-Whitney检验在多个独立样本下的推广。
  • Friedman检验：Friedman检验又被称之为双因素秩方差分析，是非参数版的anova2。同anova2一样，待检验的数据也必须是均衡的。但是需要特别注意的是，Friedman检验和anova2检验不完全相同，anova2同时注意两个因素对待检验数据的影响，但是，Friedman检验只注重2个因素中的其中一个对待检验数据的影响，而另一个因素则是用来区分区组用的。（见Frideman检验及matlab代码_friedman aligned rank代码检验-CSDN博客）

ANOVA分析的分类

根据因子数量分类

  • 单因子方差分析：用于一个因子下多个水平的均值比较。
  • 双因子方差分析：用于两个因子及其交互作用的分析。
  • 多因子方差分析：用于三个或更多因子的主效应和交互作用分析。

单因子方差分析

单因子方差分析用于比较多个组的均值，只涉及一个因子（自变量）。

例如：为了研究氮肥料使用量对水稻产量的影响，氮肥用量设低、中、高三个水平，分布使用N1，N2和N3表示

双因子方差分析

双因素方差分析分为无交互作用/有交互作用，对于有交互作用的双因素方差分析，则需要做重复实验

例如：为了研究肥料使用量对水稻产量的影响，某研究所做了氮（因素A）、磷（因素B）两种肥料施用量的二因素试验。氮肥用量设低、中、高三个水平，分布使用N1，N2和N3表示；磷肥用量设低、高2个水平，分别用P1，P2表示。

多因子方差分析

定义：多因子方差分析涉及三个或更多因子，研究它们对因变量的影响及其交互作用。

例如：研究教学方法、学习时间和学生背景（如性别、年龄）对考试成绩的影响。

根据因子类型分类

固定效应模式（Fixed-effects models）

用于方差分析模型中所考虑的因子为固定的情况，换言之，其所感兴趣的因子是来自于特定的范围。

例如，要比较五种不同的汽车销售量的差异，感兴趣的因子为五种不同的汽车，反因变量为销售量，该命题即限定了特定范围，因此模型的推论结果也将全部着眼在五种汽车的销售差异上，故此种状况下的因子便称为固定效应。

随机效应模式（Random-effects models）

不同于固定效应模式中的因子特定性，在随机效应中所考量的因子是来自于所有可能的母群体中的一组样本，因子方差分析所推论的并非着眼在所选定的因子上，而是推论到因子背后的母群体。

例如，借由一间拥有全部车厂种类的二手车公司，从所有车厂中随机挑选5种车厂品牌，用于比较其销售量的差异，最后推论到这间二手公司的销售状况。因此在随机效应模型下，研究者所关心的并非局限在所选定的因子上，而是希望借由这些因子推论背后的母群体特征。

混合效应模式（Mixed-effects models）

此种混合效应不会出现在单因子方差分析中，当双因子或多因子方差分析同时存在固定效应与随机效应时，此种模型便是典型的混合型模式。

ANOVA 分析的计算原理

Anova的核心思想是将总体方差分解为两部分：

  1. 组间方差（Between-group variance）：反映不同组别之间的差异。
  2. 组内方差（Within-group variance）：反映每个组内部的随机变异。

Anova通过比较这两种方差，计算F统计量：

F=组间方差组内方差F = \dfrac{\text{组间方差}}{\text{组内方差}}

这里的方差等于平方和除以自由度，组间的自由度为(组数-1)，组内自由度为组数*（样本量-1），方差分析各组的样本量可以不一样。

如果F值较大，说明组间差异显著大于组内随机变异，我们就有理由认为各组之间存在真实差异。

具体公式：

‍

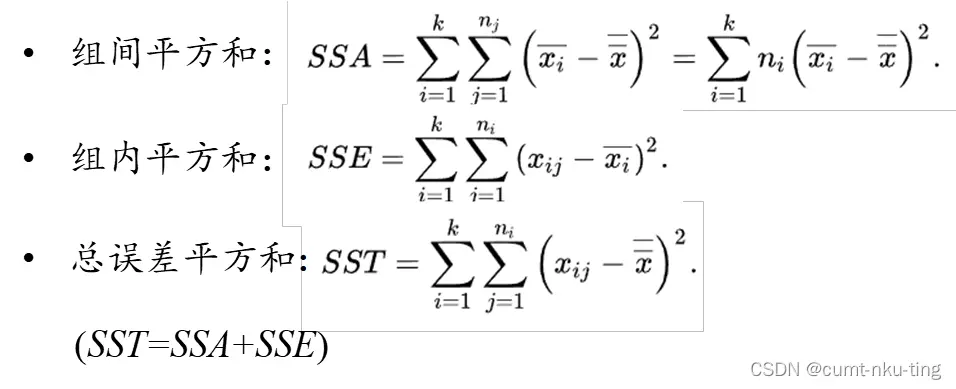
Anova的应用步骤

  1. 提出假设：

    • 零假设（H0）：所有组别的均值相等
    • 备择假设（H1）：至少有两个组别的均值不相等

  2. 收集数据并计算F值

  3. 确定显著性水平（通常为0.05）

  4. 比较计算得到的F值与临界F值

  5. 得出结论：如果计算的F值大于临界F值，则拒绝零假设，认为存在显著差异

Anova的代码实现

Matlab

文档：方差与协方差分析 - MATLAB & Simulink - MathWorks 中国

相关函数：anova、anova1、anova2、anovan

anova函数是Matlab 2022b新出的函数，可以直接执行单因素和多因素方差分析，不需要再区别使用anova1、anova2、anovan。

单因素方差分析

加载爆米花产量数据：数据为6×3 的矩阵，包含三种不同品牌的爆米花产量观测值（以杯为单位的）

1
2
load popcorn.mat
popcorn
1
2
3
4
5
6
7
8
popcorn =

    5.5000    4.5000    3.5000
    5.5000    4.5000    4.0000
    6.0000    4.0000    3.0000
    6.5000    5.0000    4.0000
    7.0000    5.5000    5.0000
    7.0000    5.0000    4.5000

进行单因素方差分析，检验爆米花产量不受爆米花品牌影响的零假设。

1
2
factors = [repmat("Gourmet",6,1); repmat("National",6,1); repmat("Generic",6,1)];
aov = anova(factors,popcorn(:),"FactorNames","Brand")
1
2
3
4
5
6
7
8
9
10
11
12
aov = 

1-way anova, constrained (Type III) sums of squares.

Y ~ 1 + Brand

             SumOfSquares    DF    MeanSquares     F        pValue  
             ____________    __    ___________    ____    __________

    Brand       15.75         2        7.875      18.9    7.9603e-05
    Error        6.25        15      0.41667                      
    Total          22        17

F 统计量的p 值足够小，可以在 0.01 的显著性水平上拒绝零假设。因此，爆米花品牌对爆米花产量有显著影响。

但是我们只知道爆米花品牌对爆米花产量有显著影响，依然不知道这几个品牌两两之间的爆米花产量有显著差异。

可以再进行多重比较：

1
multcompare(aov)
1
2
3
4
5
6
7
8
9
10
ans =

  3×6 table

      Group1        Group2      MeanDifference    MeanDifferenceLower    MeanDifferenceUpper      pValue  
    __________    __________    ______________    ___________________    ___________________    __________

    "Gourmet"     "National"          1.5               0.53198                 2.468            0.0029743
    "Gourmet"     "Generic"          2.25                 1.282                 3.218           6.3839e-05
    "National"    "Generic"          0.75              -0.21802                 1.718              0.14337

可以知道品牌1和品牌2、品牌1和品牌3有显著差异，品牌2和品牌3无显著差异

还可以绘制平均值差异，交互式查看组间差异

1
plotComparisons(aov);

蓝色代表的是当前选择的组，红色代表是与当前组显著差异的组，灰色代表的是无显著差异的组

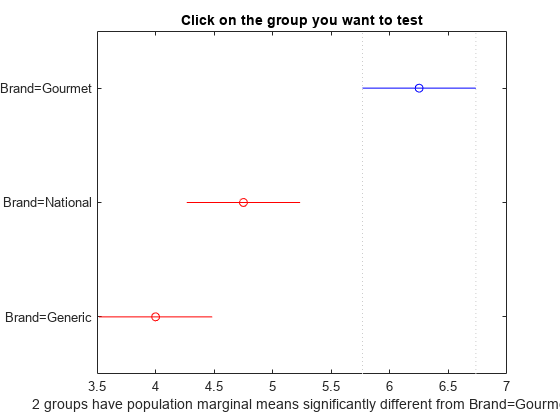
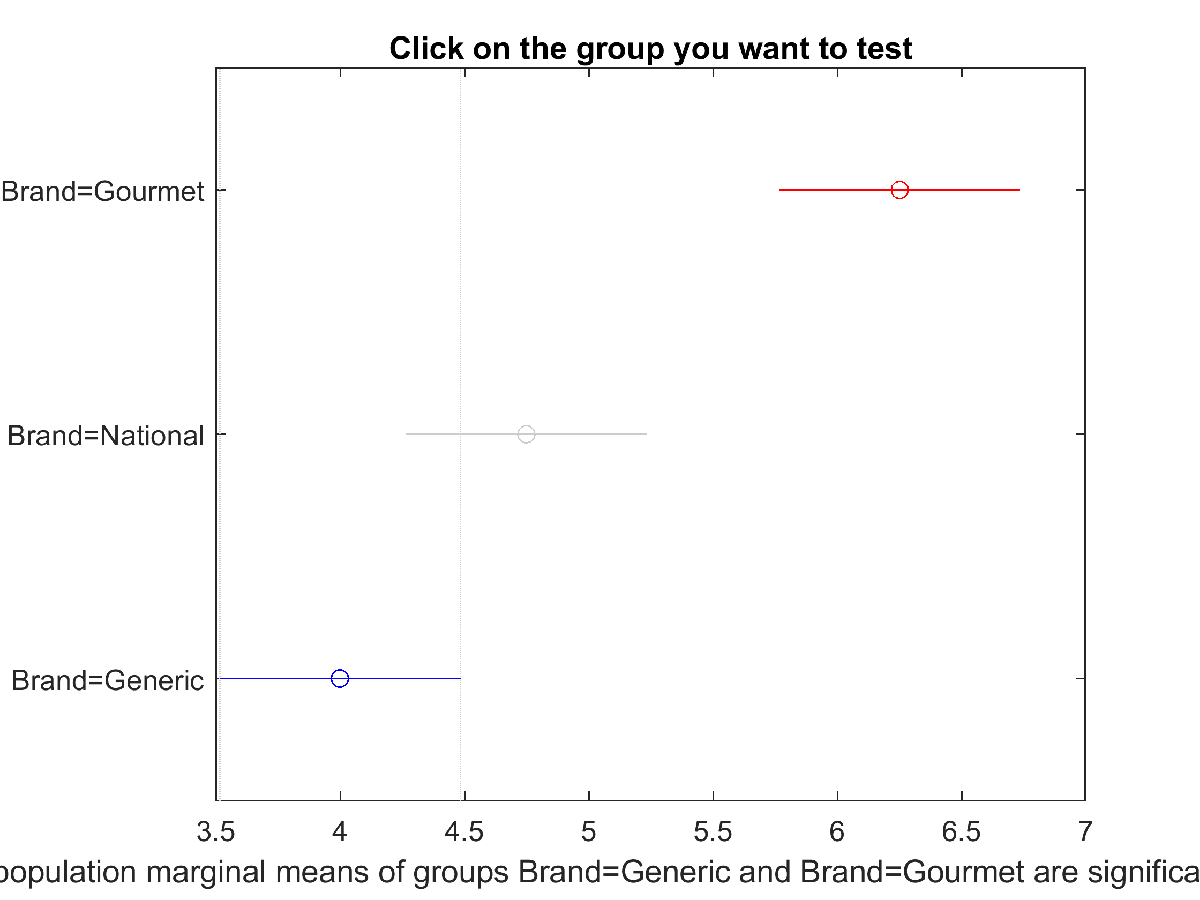
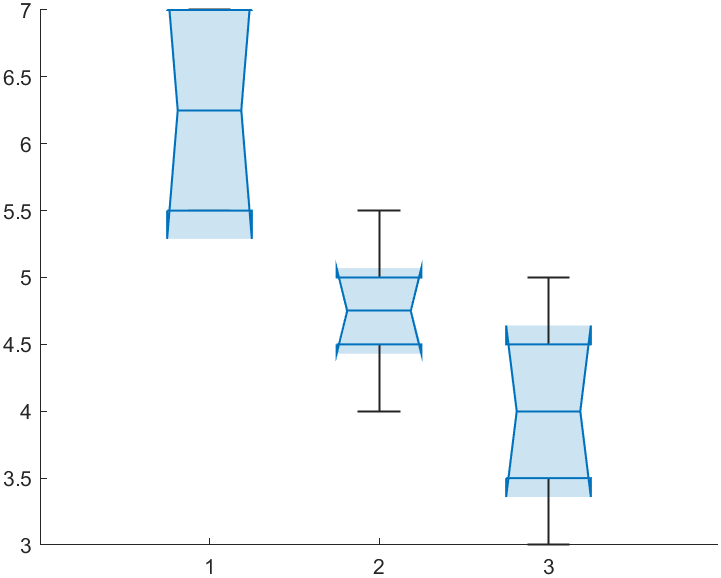
绘制箱式图

直观展示各个品牌的爆米花产量

1
boxchart(aov)

双因素方差分析

加载爆米花产量数据：数据为6×3 的矩阵，包含三种不同品牌的爆米花产量观测值（以杯为单位的）

1
2
load popcorn.mat
popcorn
1
2
3
4
5
6
7
8
popcorn =

    5.5000    4.5000    3.5000
    5.5000    4.5000    4.0000
    6.0000    4.0000    3.0000
    6.5000    5.0000    4.0000
    7.0000    5.5000    5.0000
    7.0000    5.0000    4.5000

使用repmat和table函数创建一个表格，其中包含品牌、爆米花机类型和爆米花产量的变量。

1
2
3
brand = [repmat("Gourmet",6,1);repmat("National",6,1);repmat("Generic",6,1)];
poppertype = [repmat("air",3,1);repmat("oil",3,1);repmat("air",3,1);repmat("oil",3,1);repmat("air",3,1);repmat("oil",3,1)];
tbl = table(brand,poppertype,popcorn(:),VariableNames=["Brand" "PopperType" "PopcornYield"]);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
tbl =

  18×3 table

      Brand       PopperType    PopcornYield
    __________    __________    ____________

    "Gourmet"       "air"           5.5   
    "Gourmet"       "air"           5.5   
    "Gourmet"       "air"             6   
    "Gourmet"       "oil"           6.5   
    "Gourmet"       "oil"             7   
    "Gourmet"       "oil"             7   
    "National"      "air"           4.5   
    "National"      "air"           4.5   
    "National"      "air"             4   
    "National"      "oil"             5   
    "National"      "oil"           5.5   
    "National"      "oil"             5   
    "Generic"       "air"           3.5   
    "Generic"       "air"             4   
    "Generic"       "air"             3   
    "Generic"       "oil"             4   
    "Generic"       "oil"             5   
    "Generic"       "oil"           4.5

进行双因素方差分析，零假设设置为三个品牌和两种爆米花机的爆米花产量相同。

先假设品牌和爆米花机类型是独立的，没有交互作用

1
aovLinear = anova(tbl,"PopcornYield ~ Brand + PopperType")
1
2
3
4
5
6
7
8
9
10
11
12
13
aovLinear = 
2-way anova, constrained (Type III) sums of squares.

PopcornYield ~ 1 + Brand + PopperType

                  SumOfSquares    DF    MeanSquares     F       pValue  
                  ____________    __    ___________    ___    __________

    Brand            15.75         2       7.875        63         1e-07
    PopperType         4.5         1         4.5        36    3.2548e-05
    Error             1.75        14       0.125                    
    Total               22        17

再假设品牌和爆米花机类型有交互作用

1
aovInteraction = anova(tbl,"PopcornYield ~ Brand + PopperType + Brand:PopperType")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
aovInteraction = 
2-way anova, constrained (Type III) sums of squares.

PopcornYield ~ 1 + Brand*PopperType

                        SumOfSquares    DF    MeanSquares     F        pValue  
                        ____________    __    ___________    ____    __________

    Brand                    15.75       2        7.875      56.7     7.679e-07
    PopperType                 4.5       1          4.5      32.4    0.00010037
    Brand:PopperType      0.083333       2     0.041667       0.3       0.74622
    Error                   1.6667      12      0.13889                      
    Total                       22      17


aovInteraction的方差分析模型包括交互项Brand:PopperType。Brand:PopperType项的p 值大于 0.05。因此，没有足够证据证明品牌和爆米花机类型对爆米花产量有交互影响。

anova对象的Metrics属性提供了有关方差分析模型拟合度的统计数据。要确定哪种模型更适合响应数据，请显示aovLinear和aovInteraction 的Metrics属性。

1
aovLinear.Metrics
1
2
3
4
5
6
ans=1×7 table
     MSE      RMSE      SSE      SSR     SST    RSquared    AdjustedRSquared
    _____    _______    ____    _____    ___    ________    ________________

    0.125    0.35355    1.75    20.25    22     0.92045         0.88731   

1
aovInteraction.Metrics
1
2
3
4
5
ans=1×7 table
      MSE       RMSE       SSE       SSR      SST    RSquared    AdjustedRSquared
    _______    _______    ______    ______    ___    ________    ________________

    0.13889    0.37268    1.6667    20.333    22     0.92424         0.78535

线性模型的均方误差（MSE）略小于交互模型。线性模型的调整 R 平方值更高。这些指标共同表明，线性模型比交互模型更适合爆米花数据。

随机效应ANOVA

我记录了大鼠不同行为（移动、饲养、梳理…）的钙信号（使用纤维光度计），每只大鼠的每种行为都有很多次，每次记录时间为 5 分钟（每次记录相隔几天）。

分析时间、行为、大鼠编号、每次记录对钙信号的影响

由于每只老鼠都是一个随机因素，每次会话也是一个随机因素，所以将其设置为随机效应因子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
% 生成随机数据
tbl = table(randn(100,1), (1:100)', randi([1,3],100,1), ...
            randi([1,10],100,1), randi([1,20],100,1), ...
            'VariableNames', {'CalciumResponse', 'Time', 'Behavior', 'Rat', 'Session'});
tbl.Behavior = categorical(tbl.Behavior);
tbl.Rat = categorical(tbl.Rat);
tbl.Session = categorical(tbl.Session);
% Perform  ANOVA with Random Effects
aov = anova(tbl, 'CalciumResponse', ...
            'CategoricalFactors', [2,3,4], ...
            'RandomFactors', [3,4]);


aov = anova(tbl, 'CalciumResponse ~ Time * Behavior + Rat + Session', ...
            'CategoricalFactors', [2,3,4], ...
            'RandomFactors', [3,4]);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
aov = 

N-way anova, constrained (Type III) sums of squares.

CalciumResponse ~ 1 + Rat + Session + Time*Behavior

                     SumOfSquares    DF    MeanSquares       F       pValue 
                     ____________    __    ___________    _______    _______

    Time               0.63547        1      0.63547      0.59586    0.44292
    Behavior            1.2215        2      0.61076      0.57269    0.56678
    Rat                 8.0684        9      0.89649      0.84061    0.58172
    Session             16.935       19      0.89133      0.83577    0.65822
    Time:Behavior       1.1771        2      0.58853      0.55184    0.57852
    Error               70.387       66       1.0665                      
    Total               97.922       99   
1
[~,ems] = stats(aov)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
ems =

  6×5 table

                       Type                      ExpectedMeanSquares                    MeanSquaresDenominator    DFDenominator    FDenominator
                     ________    ___________________________________________________    ______________________    _____________    ____________

    Time             "fixed"     "54736.8*Q(Time)+18245.6*Q(Time:Behavior)+V(Error)"            1.0665                  66          MS(Error)  
    Behavior         "fixed"     "6.00085*Q(Behavior)+V(Error)"                                 1.0665                  66          MS(Error)  
    Rat              "random"    "7.83495*V(Rat)+V(Error)"                                      1.0665                  66          MS(Error)  
    Session          "random"    "4.30322*V(Session)+V(Error)"                                  1.0665                  66          MS(Error)  
    Time:Behavior    "fixed"     "20371.8*Q(Time:Behavior)+V(Error)"                            1.0665                  66          MS(Error)  
    Error            "random"    "V(Error)"

参考

许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

快来参与讨论吧~