假设检验丨Wilcoxon Signed Rank Test（Wilcoxon符号秩检验）

Wilcoxon符号秩检验一种非参数统计检验方法，主要用于比较两个配对样本观测值之间的差异。它是sign test（符号检验）的改进，是在观察“+”“-”号个数的基础上亦考虑差值的大小，通过对差值偏秩求和进行检验的。Wilcoxon符号秩检验是替代「配对t检验」的非参数方法，适用于数据不满足正态分布的情况。

💡总结Wilcoxon符号秩检验和其他检验方法的关系

• Wilcoxon符号秩检验与Mann-Whitney U检验：两者都是非参数检验方法，Wilcoxon用于配对样本，Mann-Whitney U用于独立样本
• Wilcoxon符号秩检验与配对t检验：Wilcoxon是配对t检验的非参数替代方法
• Wilcoxon符号秩检验与符号检验（Sign test）：Wilcoxon符号秩检验是符号检验的改进版本，Wilcoxon符号秩检验考虑了差值的大小，而符号检验仅考虑正负号

适用条件

• 数据为连续型或有序的离散型。
• 两个样本是配对的，即每对数据点之间是相关的。
• 数据不需要服从正态分布，但假设数据是对称的。

基本思想

首先计算配对数据差值，然后对差值的绝对值进行排序并赋予秩次，最后分别计算正秩次之和与负秩次之和。通过比较正秩和与负秩和的大小来判断两组数据是否存在显著差异。

例子

电解法和分光光度法测试样本浓度有没有差异？

Wilcoxon配对符号秩和检验｜说人话的统计学_哔哩哔哩_bilibili

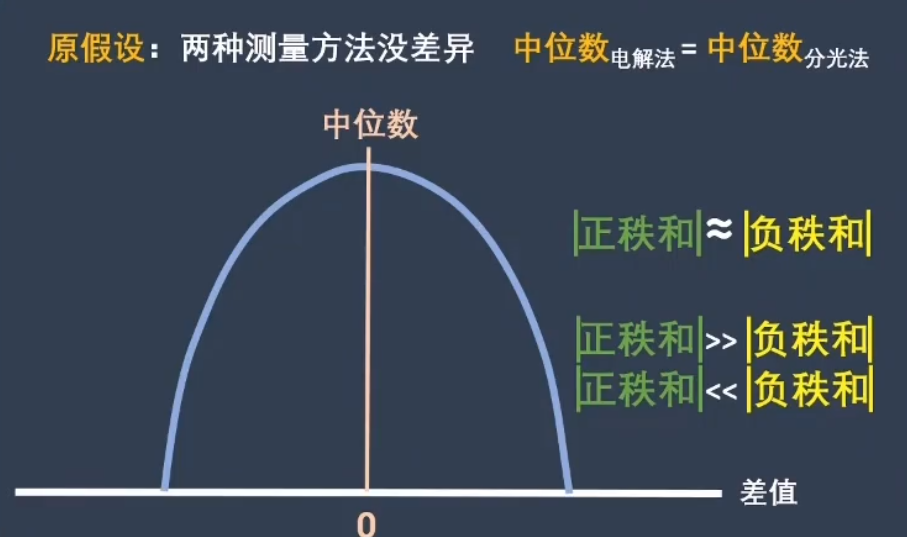
现在要测量污水里面氟离子的浓度，有两种测量方法，分别对11个污水样本进行测量。这是测量的结果，我们想知道两种测量结果是否一致。

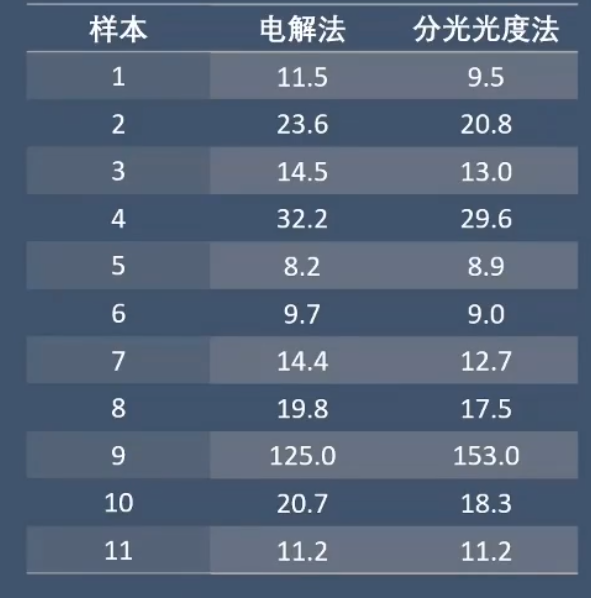
按照以往的经验，会考虑用配对T检验。如果对这个检验方法不了解，可以翻看前面的视频。但配对T检验有个前提：数据要服从正态分布。根据频率直方图和正态性测试，这些数据明显不服从正态。

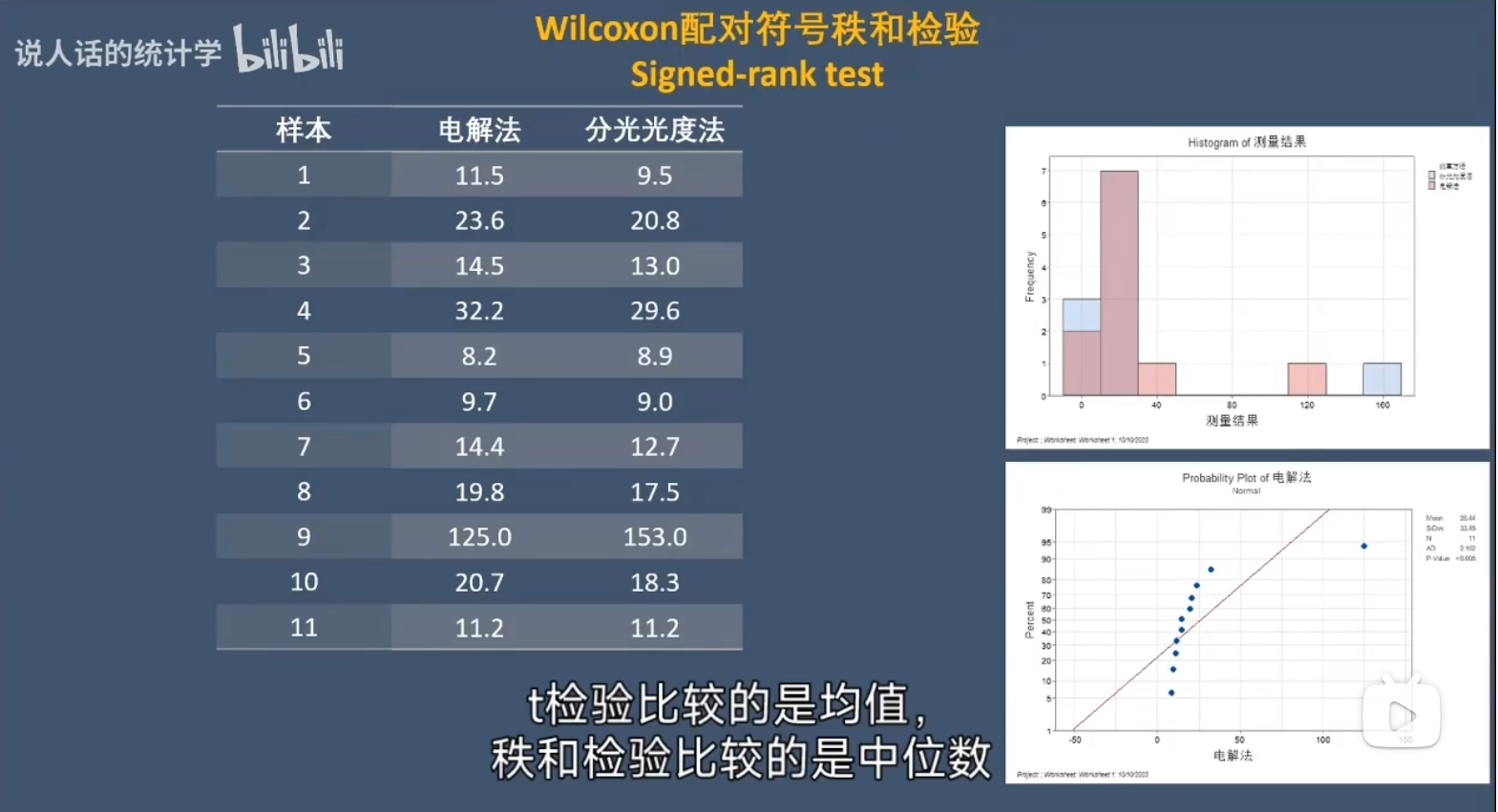
既然不能用配对T检验，那就用一个没有正态分布要求的检验方法吧。Wilcoxon配对符号秩和检验比较的是**中位数，而T检验比较的是均值**。

配对比较是计算每个样本的两种测量结果的差值。当然差值有正负之分，然后对这些差值按照绝对值的大小，从小到大排序。

• 首先，差值为零的不参与排序。
• 绝对值最小的两个差值占了前两位，那到底谁是第一，谁是第二呢？别抢了，大家都取中间值1.5，但要注意秩次也有正负。
• 排第三的是它，排第四和第五的是这两个样本。同理把所有的秩次都计算出来，现在把正的和负的秩和求和，得到正秩和与负秩和。

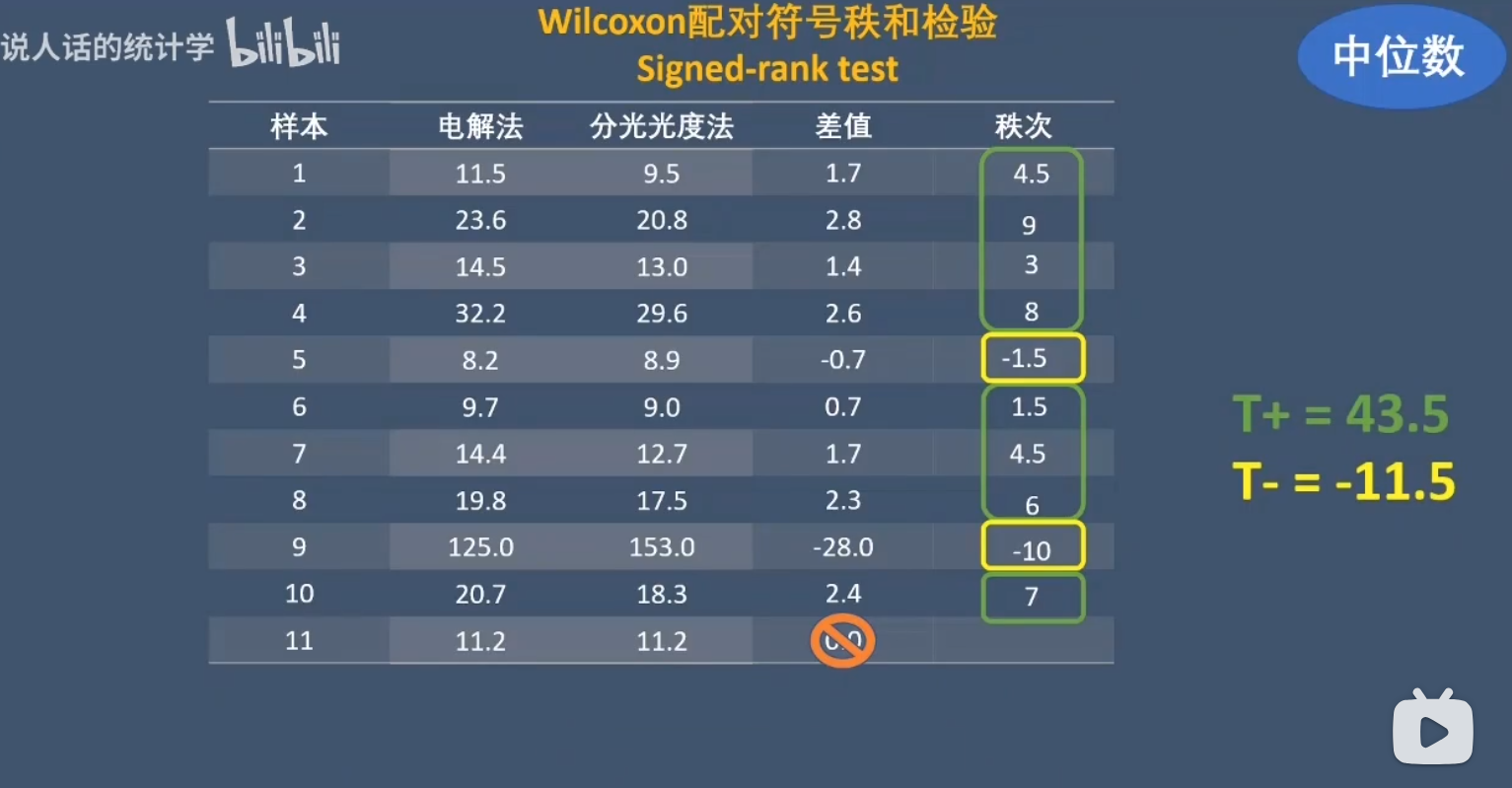
我们的原假设是两种测量方法没有差异，也就是总体的中位数相同。如果两种测量方法真的没有差异，同一个样本的测量结果要么你大，要么我大，都是很随机的。所以差值的分布应该是大体左右对称的吧，而且这个**差值分布**的中位数应该等于零，正秩和和负秩和的绝对值应该差别不大。如果样本的计算结果告诉我，两个值的大小差很远，那就有理由怀疑原假设的真实性了，拒绝原假设。

航行对心率有无影响

drhuang.com/chinese/health/medicine/book/预防医学/577.htm

治疗前后

The Wilcoxon signed-rank test & the sign test (youtube.com)

代码实现

Matlab

文档：signrank

在 MATLAB 中，你可以使用 signrank 函数进行 Wilcoxon 符号秩检验。

1
2
3
4
5
6
7
8
9
10
11
12
13

% 生成数据
rng(42); % 设置随机种子
n = 20;
data_before = normrnd(50, 10, [1, n]);
data_after = data_before + normrnd(0, 5, [1, n]);

% Wilcoxon 符号秩检验
[p, h, stats] = signrank(data_before, data_after);

% 输出结果
fprintf('p-value: %f\n', p);
disp(stats);

Python

在 Python 中，你可以使用 scipy.stats.wilcoxon 函数进行 Wilcoxon 符号秩检验。

1
2
3
4
5
6
7

pythonfrom scipy.stats import wilcoxon

# Wilcoxon 符号秩检验
stat, p_value = wilcoxon(data_before, data_after)

# 输出结果
print(f'p-value: {p_value}')

R

在 R 中，你可以使用 wilcox.test 函数进行 Wilcoxon 符号秩检验。

1
2
3
4
5
6
7
8
9
10
11

r# 生成数据
set.seed(42) # 设置随机种子
n <- 20
data_before <- rnorm(n, mean=50, sd=10)
data_after <- data_before + rnorm(n, mean=0, sd=5)

# Wilcoxon 符号秩检验
test_result <- wilcox.test(data_before, data_after, paired=TRUE)

# 输出结果
print(test_result)

问题

• 如何确定数据是对称分布的

  1. 绘制图形
  • 直方图（Histogram） ：
    直方图可以直观地展示数据的分布情况。对称分布的直方图通常呈现为中间高、两边低的形状，类似于钟形曲线。
  • 盒须图（Boxplot） ：
    盒须图可以帮助判断数据的对称性。对称分布的盒须图中位数线应该位于盒子的中央，两边的须长度相似。
  2. 计算统计量
  • 偏度（Skewness） ：
    偏度是衡量数据分布对称性的统计量。偏度接近于零表示数据接近对称分布。计算偏度的公式为：
  • 峰度（Kurtosis） ：
  3. 正态性检验

  虽然正态分布并不完全等同于对称分布，但正态性检验可以作为一种辅助工具。

  • Shapiro-Wilk Test：
    Shapiro-Wilk检验用于检验数据是否来自正态分布。p值大于0.05则无法拒绝原假设，表示数据可能是正态分布，从而可能是对称分布。
  • Kolmogorov-Smirnov Test：
    KS检验也可用于正态性检验，同样p值大于0.05表示数据可能是正态分布。

‍